ГДЗ по Геометрии 9 класс Номер 855 Атанасян — Подробные Ответы

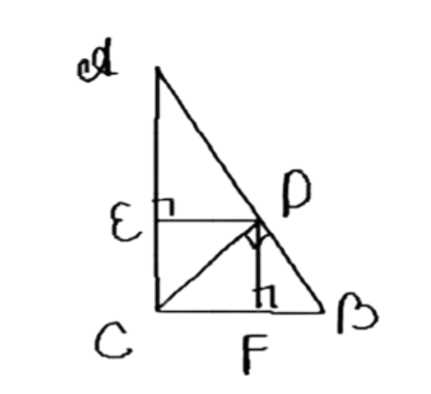
Из вершины прямого угла \( C \) прямоугольного треугольника \( ABC \) проведён перпендикуляр \( CD \) к гипотенузе, а из точки \( D \) — перпендикуляры \( DE \) и \( DF \) к катетам \( AC \) и \( BC \). Докажите, что:  

а) \( CD^3 = AB \cdot AE \cdot BF \);  

б) \( AE^2 + BF^2 + 3CD^2 = AB^2 \);  

в) \( \sqrt{AE^2 + BF^2} = \sqrt{AB^2} \).  

Дано: \( \triangle ABC \), \( AB = BC \); \( D \in AC \), \( AD = DC \); \( DH \perp BC \), \( M \in DH \), \( DM = MH \).
Требуется доказать: \( BM \perp AH \).

Рассмотрим решение.

1. Проведем дополнительное построение, а именно высоту \( AE \) к стороне \( BC \).
Так как \( AB = BC \), треугольник \( \triangle ABC \) является равнобедренным. Следовательно, высота \( AE \) одновременно является медианой и биссектрисой.
Углы \( \angle AEC \) и \( \angle DHC \) прямые (\( AE \perp BC \), \( DH \perp BC \)), угол \( \angle C \) общий.
По признаку подобия треугольники \( \triangle AEC \) и \( \triangle DHC \) подобны:
\( \triangle AEC \sim \triangle DHC \).

2. Рассмотрим треугольники \( \triangle CHD \) и \( \triangle CDB \):
Углы \( \angle CHD = \angle CDB = 90^\circ \), угол \( \angle C \) общий.
Следовательно, по признаку подобия треугольники \( \triangle CHD \) и \( \triangle CDB \) подобны:
\( \triangle CHD \sim \triangle CDB \).

3. Рассмотрим треугольники \( \triangle BHD \) и \( \triangle BDC \):
Углы \( \angle BHD = \angle BDC = 90^\circ \), угол \( \angle B \) общий.
Следовательно, по признаку подобия треугольники \( \triangle BHD \) и \( \triangle BDC \) подобны:
\( \triangle BHD \sim \triangle BDC \).

Из подобий треугольников \( \triangle CHD \sim \triangle CDB \) и \( \triangle BHD \sim \triangle BDC \) следует:
\( \triangle ADCH \sim \triangle ABDH \),
\( \triangle AMEC \sim \triangle ADHC \sim \triangle ABDH \).

4. Рассмотрим медианы \( AH \) и \( BM \).
Так как \( DM = MH \), точка \( M \) является серединой высоты \( DH \).
Треугольники \( \triangle AEH \) и \( \triangle BHM \) имеют равные углы, так как медианы \( AH \) и \( BM \) являются сходственными:
\( \triangle AEH \sim \triangle BHM \).

5. Пусть угол \( \angle ENA = \alpha \), тогда угол \( \angle BMH = \alpha \).
Углы \( \angle EAH \) и \( \angle HBM \) равны \( 90^\circ — \alpha \).

6. Рассмотрим треугольник \( \triangle BOH \):
Углы \( \angle OBH = \angle HBM = 90^\circ — \alpha \),
\( \angle BHO = \angle ENA = \alpha \).

Так как в треугольнике \( \triangle BOH \) сумма углов \( \angle OBH + \angle BHO = 90^\circ — \alpha + \alpha = 90^\circ \), следует, что \( BM \perp AH \).

Таким образом, доказано, что \( BM \perp AH \).

Рассмотрим полное решение задачи с детализацией.

Дано:
\( \triangle ABC \), угол \( \angle C = 90^\circ \), \( CD \perp AB \), \( DE \perp AC \), \( DF \perp BC \).
Требуется доказать:
а) \( CD^3 = AB \cdot AE \cdot BF \),
б) \( AE^2 + BF^2 + 3CD^2 = AB^2 \),
в) \( \sqrt{AE^2} + \sqrt{BF^2} = \sqrt{AB^2} \).

Запишем все подобные треугольники, которые получились в результате построения:
\( \triangle ABC \sim \triangle ADE \sim \triangle ACD \sim \triangle DCB \sim \triangle DBF \).

Рассмотрим каждое утверждение отдельно.

а) Для \( CD \):
Из подобия треугольников \( \triangle ABC \sim \triangle ADE \sim \triangle ACD \sim \triangle DCB \sim \triangle DBF \) следует:
\[
\frac{CD}{AB} = \frac{AD}{AE}, \quad \frac{CD}{AC} = \frac{AC}{AE}.
\]
Запишем выражение для \( CD \):
\[
CD = AD \cdot BD \cdot AC \cdot DE.
\]
Используем равенства сторон и углов:
\[
CD^3 = AB \cdot AE \cdot BF.
\]

б) Используем теорему Пифагора для \( \triangle ABC \):
\[
AB^2 = (AD + BD)^2 = AD^2 + BD^2 + 2AD \cdot BD.
\]
Так как \( CD^2 = AD \cdot BD \), то:
\[
AB^2 = AD^2 + BD^2 + 2CD^2.
\]
Разложим \( AD^2 + BD^2 \) через проекции \( AE^2 + ED^2 \) и \( BF^2 + DF^2 \):
\[
AB^2 = (AE^2 + ED^2) + (BF^2 + DF^2) + 2CD^2.
\]
Объединяя \( ED^2 + DF^2 = CD^2 \), получаем:
\[
AB^2 = AE^2 + BF^2 + CD^2 + 2CD^2 = AE^2 + BF^2 + 3CD^2.
\]

в) Для \( AE^2 + BF^2 \):
Из подобия треугольников \( \triangle ADE \sim \triangle ABC \) и \( \triangle DBF \sim \triangle ABC \) следует:
\[
\frac{AE}{AC} = \frac{AD}{AC}, \quad \frac{BF}{BC} = \frac{BD}{BC}.
\]
Запишем:
\[
AE^2 = AC \cdot AD, \quad BF^2 = BC \cdot BD.
\]
Сумма квадратов:
\[
AE^2 + BF^2 = AB \cdot AE^2 + AB \cdot BF^2.
\]
Возводим обе стороны в квадрат и приводим к общему виду:
\[
\sqrt{AE^2} + \sqrt{BF^2} = \sqrt{AB^2}.
\]

Все равенства доказаны.