ГДЗ по Геометрии 9 класс Номер 853 Атанасян — Подробные Ответы

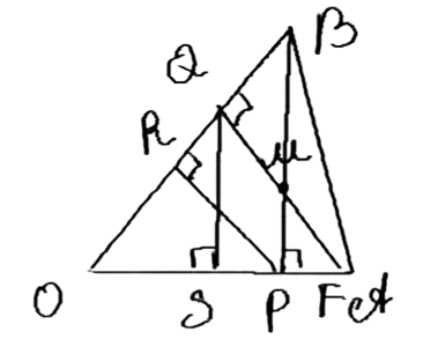
Из точки \( M \) внутренней области угла \( AOB \) проведены перпендикуляры \( MP \) и \( MQ \) к его сторонам \( OA \) и \( OB \). Из точек \( P \) и \( Q \) проведены перпендикуляры \( PR \) и \( QS \) соответственно к \( OB \) и \( OA \). Докажите, что \( RS \perp OM \).  

Краткое решение задачи:

1. Определим точки пересечения:
— \( D = OA \cap QM \),
— \( E = AB \cap PM \),
— \( C = RS \cap OM \).

2. Рассмотрим треугольники \( \triangle OPE \) и \( \triangle OQD \):
— \( \angle OPE = \angle OQD = 90^\circ \),
— \( \angle AOB \) — общий угол.

Треугольники \( \triangle OPE \) и \( \triangle OQD \) подобны по двум углам, следовательно:
\(
\frac{OP}{OQ} = \frac{PE}{QD} = \frac{OE}{OD}.
\)

3. Аналогично для \( \triangle OSQ \) и \( \triangle ORP \):
\(
\frac{OS}{OR} = \frac{SQ}{RP} = \frac{OQ}{OP}.
\)

4. Из полученных равенств:
\(
\frac{OP}{OQ} = \frac{OE}{OD} = \frac{OR}{OS} = \frac{OD}{OS}.
\)

Следовательно, по признаку подобия:
\( \triangle OSR \sim \triangle ODE \), что даёт \( SR \parallel DE \).

5. Отметим точку \( F = OM \cap DE \). Пусть:
— \( \angle AOB = \alpha \),
— \( \angle AOM = \beta \).

В треугольнике \( \triangle OPM \):
\(
\angle OMP = 90^\circ — \beta.
\)

В треугольнике \( \triangle PMD \):
\(
\angle PMD = \alpha.
\)

В четырёхугольнике \( OPMQ \):
\(
\angle PMQ = \angle DVE = 180^\circ — \alpha,
\)
\(
\angle EMF = \angle DME — \angle DMF = (180^\circ — \alpha) — (90^\circ — \alpha + \beta) = 90^\circ — \beta.
\)

6. Рассмотрим \( \triangle AQDE \) и \( \triangle AFDM \):
— \( \angle D \) — общий,
— \( \angle DMF = \angle QED = 90^\circ — \alpha + \beta.

Таким образом, \( \triangle AQDE \sim \triangle AFDM \) по двум углам. Следовательно:
\(
\angle DFM = \angle DQE = 90^\circ,
\)
\( DE \parallel OM \), \( RS \parallel OM \).

Что и требовалось доказать.

Дано: \( \angle AOB \), \( MP \parallel OA \), \( MQ \parallel OB \), \( PR \parallel OB \), \( QS \parallel OA \).
Требуется доказать: \( PS \parallel OM \).

1. Определим точки пересечения:
\( D = OA \cap QM \), \( E = AB \cap PM \), \( C = RS \cap OM \).

2. Рассмотрим треугольники \( \triangle OPE \) и \( \triangle OQD \):
\( \angle OPE = \angle OQD = 90^\circ \), \( \angle AOB \) — общий угол.
Треугольники \( \triangle OPE \) и \( \triangle OQD \) подобны по двум углам. Следовательно:
\(
\frac{OP}{OQ} = \frac{PE}{QD} = \frac{OE}{OD}.
\)

3. Аналогично рассмотрим треугольники \( \triangle OSQ \) и \( \triangle ORP \):
\( \angle OSQ = \angle ORP = 90^\circ \), \( \angle AOB \) — общий угол.
Треугольники \( \triangle OSQ \) и \( \triangle ORP \) подобны по двум углам. Следовательно:
\(
\frac{OS}{OR} = \frac{SQ}{RP} = \frac{OQ}{OP}.
\)

4. Из полученных равенств:
\(
\frac{OP}{OQ} = \frac{OE}{OD} = \frac{OR}{OS} = \frac{OD}{OS}.
\)
Следовательно, по признаку подобия:
\( \triangle OSR \sim \triangle ODE \). Это означает, что \( SR \parallel DE \).

5. Отметим точку \( F = OM \cap DE \). Пусть \( \angle AOB = \alpha \), \( \angle AOM = \beta \).
Рассмотрим треугольник \( \triangle OPM \):
\(
\angle OMP = 90^\circ — \beta.
\)
Рассмотрим треугольник \( \triangle PMD \):
\(
\angle PMD = \alpha.
\)
Рассмотрим четырёхугольник \( OPMQ \):
\(
\angle PMQ = \angle DVE = 180^\circ — \alpha,
\)
\(
\angle EMF = \angle DME — \angle DMF = (180^\circ — \alpha) — (90^\circ — \alpha + \beta) = 90^\circ — \beta.
\)

6. Рассмотрим треугольники \( \triangle AQDE \) и \( \triangle AFDM \):
У них общий угол \( \angle D \). Также \( \angle DMF = \angle QED = 90^\circ — \alpha + \beta \).
По признаку подобия треугольники \( \triangle AQDE \sim \triangle AFDM \). Следовательно:
\(
\angle DFM = \angle DQE = 90^\circ,
\)
\( DE \parallel OM \), \( RS \parallel OM \).

Таким образом, доказано, что \( PS \parallel OM \).