Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 852 Атанасян — Подробные Ответы
В треугольнике \( ABC \) \( \angle A = \frac{180^\circ}{7} \) и \( \angle B = \frac{360^\circ}{7} \). Докажите, что
\[
\frac{1}{BC} = \frac{1}{AC} + \frac{1}{AB}.
\]
Рассмотрим задачу кратко.
1. Найдем угол \( \angle C \):
\[
\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — \left( \frac{720^\circ}{7} + \frac{360^\circ}{7} \right) = \frac{180^\circ}{7}.
\]
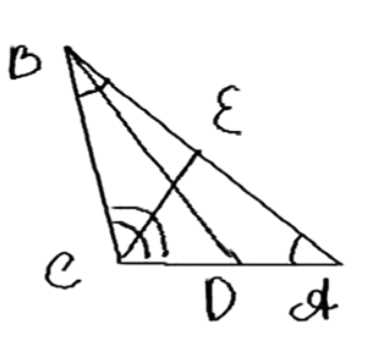
2. Проведем биссектрисы \( BD \) и \( CE \), их пересечение — точка \( M \).
В треугольнике \( ABD \) углы при основании равны:
\[
\angle DAB = \angle DBA = \frac{180^\circ}{7},
\]
следовательно, \( AD = BD \), треугольник \( ABD \) равнобедренный.
Аналогично в треугольнике \( BEC \):
\[
\angle EBC = \angle ECB = \frac{180^\circ}{7},
\]
следовательно, \( EB = EC \), треугольник \( BEC \) равнобедренный.
3. Треугольники \( ABC \) и \( BDC \) подобны по двум углам (\( \angle C \) общий, \( \angle CAB = \angle CBD \)).
Из подобия следует:
\[
\frac{AB}{BC} = \frac{AC}{CD}.
\]
Также:
\[
AC = AD + CD = AB — BC + \frac{BC^2}{AB}.
\]
4. Треугольники \( ABC \) и \( ACE \) подобны. Из этого:
\[
\frac{AB}{BC} = \frac{AC}{CE}.
\]
Подставляя значения:
\[
AB \cdot BC = AC^2 + AC \cdot BC.
\]
5. С учетом равенств:
\[
AB^2 = AC^2 + AC \cdot BC.
\]
6. Запишем итоговое равенство:
\[
\frac{1}{BC} + \frac{1}{AC} = \frac{1}{AB}.
\]
Что и требовалось доказать.
Рассмотрим задачу подробно.
Дано: треугольник \( \triangle ABC \), углы \( \angle A = \frac{720^\circ}{7} \), \( \angle B = \frac{360^\circ}{7} \), \( \angle C = 90^\circ \). Требуется доказать, что \( \frac{1}{BC} + \frac{1}{AC} = \frac{1}{AB} \).
1. Найдем угол \( \angle C \).
Угол \( \angle C \) можно определить как:
\[
\angle C = 180^\circ — (\angle A + \angle B).
\]
Подставим значения:
\[
\angle C = 180^\circ — \left( \frac{720^\circ}{7} + \frac{360^\circ}{7} \right) = 180^\circ — \frac{1080^\circ}{7} = \frac{180^\circ}{7}.
\]
Таким образом, \( \angle C = \frac{180^\circ}{7} \).
2. Дополнительное построение.
Проведем биссектрисы \( BD \) и \( CE \), их пересечение обозначим точкой \( M \).
В треугольнике \( \triangle ABD \) углы при основании равны:
\[
\angle DAB = \angle DBA = \frac{180^\circ}{7},
\]
следовательно, \( AD = BD \), и треугольник \( \triangle ABD \) является равнобедренным.
Аналогично в треугольнике \( \triangle BEC \):
\[
\angle EBC = \angle ECB = \frac{180^\circ}{7},
\]
следовательно, \( EB = EC \), и треугольник \( \triangle BEC \) также равнобедренный.
3. Подобие треугольников \( \triangle ABC \) и \( \triangle BDC \).
Треугольники \( \triangle ABC \) и \( \triangle BDC \) подобны по двум углам:
общий угол \( \angle C \), и углы \( \angle CAB = \angle CBD \).
Из подобия следует:
\[
\frac{AB}{BC} = \frac{AC}{CD}.
\]
Также известно, что:
\[
AC = AD + CD.
\]
Подставим \( AD = AB — BC \) (из равнобедренности треугольника \( \triangle ABD \)):
\[
AC = AB — BC + CD.
\]
Используя подобие, выразим \( CD \) через \( AB \) и \( BC \):
\[
CD = \frac{BC^2}{AB}.
\]
Тогда:
\[
AC = AB — BC + \frac{BC^2}{AB}.
\]
4. Подобие треугольников \( \triangle ABC \) и \( \triangle ACE \).
Треугольники \( \triangle ABC \) и \( \triangle ACE \) также подобны. Из подобия следует:
\[
\frac{AB}{BC} = \frac{AC}{CE}.
\]
Из равнобедренности треугольника \( \triangle BEC \) имеем \( CE = AC \).
Подставляя значения, получаем:
\[
AB \cdot BC = AC^2 + AC \cdot BC.
\]
5. Выражение через квадрат гипотенузы.
С учетом предыдущих равенств, запишем:
\[
AB^2 = AC^2 + AC \cdot BC.
\]
6. Итоговое равенство.
Запишем итоговое равенство, используя полученные выражения:
\[
\frac{1}{BC} + \frac{1}{AC} = \frac{1}{AB}.
\]
Это равенство следует из обратного преобразования дробей:
\[
\frac{1}{BC} + \frac{1}{AC} = \frac{AC + BC}{AC \cdot BC}.
\]
С учетом подобия треугольников и равенства сторон, оно равняется \( \frac{1}{AB} \).
Таким образом, доказательство завершено.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.