ГДЗ по Геометрии 9 класс Номер 851 Атанасян — Подробные Ответы

Гипотенуза прямоугольного треугольника является стороной квадрата, не перекрывающегося с этим треугольником. Найдите расстояние от точки пересечения диагоналей квадрата до вершины прямого угла треугольника, если сумма катетов равна \( a \).

Рассмотрим решение задачи:

1. Проведем дополнительные построения. Перпендикуляры из точки \( O \): \( OM \perp CB \), \( OK \perp AC \).

2. Рассмотрим треугольники \( \triangle AOK \) и \( \triangle BOM \). По построению:
\( OA = OB \) — диагональ квадрата,
\( \angle AKO = \angle BMO = 90^\circ \),
\( AO \perp OB \), \( KO \perp OM \),
\( \triangle AOK \cong \triangle BOM \) по гипотенузе и острому углу.

3. Из равенства треугольников следует:
\( AK = BM \),
\( AC + BC = AC + CM = a \),
\( OK = OM \),
\( CKOM \) — квадрат.
Следовательно, \( KC = CM = \frac{a}{2} \).

4. Поскольку \( OC \) — диагональ квадрата \( CKOM \), то:
\( OC = KC \cdot \sqrt{2} = \frac{a}{2} \cdot \sqrt{2} = \frac{a\sqrt{2}}{2} \).

Ответ: \( \frac{a\sqrt{2}}{2} \).

Рассмотрим задачу подробно и детализируем решение.

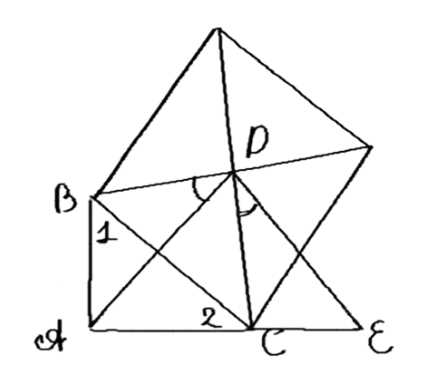
Дано: \(\triangle ABC\), \(\angle C = 90^\circ\), \(ABDF\) — квадрат, \(O = AD \cap BE\), \(AC + BC = a\).
Найти: \(OC\).

1. Сделаем дополнительное построение: проведем перпендикуляры из точки \(O\):
\(OM \perp CB\), \(OK \perp AC\).
Эти перпендикуляры пересекают стороны \(\triangle ABC\) в точках \(M\) и \(K\) соответственно.

2. Рассмотрим треугольники \(\triangle AOK\) и \(\triangle BOM\). По условию:
\(OA = OB\), так как \(O\) — центр квадрата \(ABDF\), а \(OA\) и \(OB\) равны диагоналям квадрата.
Углы \(\angle AKO = \angle BMO = 90^\circ\), так как \(OK \perp AC\) и \(OM \perp CB\).
Кроме того, \(\angle AOK = \angle BOM\), так как они вертикальные.

Следовательно, \(\triangle AOK \cong \triangle BOM\) по гипотенузе (\(OA = OB\)) и одному острому углу (\(\angle AOK = \angle BOM\)).

3. Из равенства треугольников \(\triangle AOK\) и \(\triangle BOM\) следует, что:
\(AK = BM\), \(OK = OM\).
Также известно, что \(AC + BC = a\).
Поскольку \(AC = AK + KC\) и \(BC = BM + MC\), то:
\(AC + BC = AK + KC + BM + MC = a\).
Так как \(AK = BM\), то \(KC = MC = \frac{a}{2}\).

4. Рассмотрим квадрат \(CKOM\), образованный точками \(C\), \(K\), \(O\), \(M\).
Стороны квадрата равны: \(KC = CM = \frac{a}{2}\).
Диагональ квадрата \(OC\) выражается через его сторону по формуле:
\[
OC = KC \cdot \sqrt{2}.
\]
Подставим значение \(KC = \frac{a}{2}\):
\[
OC = \frac{a}{2} \cdot \sqrt{2} = \frac{a\sqrt{2}}{2}.
\]

Ответ: \(OC = \frac{a\sqrt{2}}{2}\).