Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 850 Атанасян — Подробные Ответы
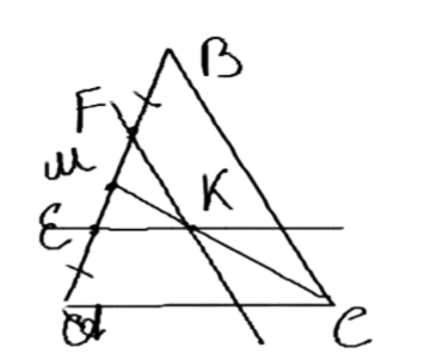
Точки \( E \) и \( F \) лежат на стороне \( AB \) треугольника \( ABC \), причём точка \( E \) лежит на отрезке \( AF \) и \( AE = BF \). Прямая, проведённая через точку \( E \) параллельно стороне \( AC \), пересекает прямую, проведённую через точку \( F \) параллельно стороне \( BC \), в точке \( K \). Докажите, что точка \( K \) лежит на медиане треугольника \( ABC \), проведённой к стороне \( AB \).
Рассмотрим доказательство:
1) Пусть \(AM = MB = d\), \(AE = FM = f\). Тогда \(EM = MF = d — f\), так как \(KM\) — медиана треугольника \(EFK\).
2) Выполним дополнительное построение. Пусть \(D = AC \cap FK\), \(G = BC \cap EK\) — точки пересечения.
3) Четырехугольник \(KGCD\) — параллелограмм, а \(KC\) — его диагональ. Следовательно, \(\angle DCG = \angle DKG = \angle C\).
4) Достроим \(AEFK\) до параллелограмма \(EHFK\), где точка \(M\) делит диагонали пополам и находится на прямой \(KH\).
5) По построению \(HF \parallel AC\). Для секущей \(AC\) имеем: \(D \in FK\), \(\angle ACH = \angle HFD = \angle HFK\). Также для секущей \(EK\) имеем: \(\angle EKH = \angle CHFK\), тогда \(\angle ACH = \angle EKH\), \(EK \parallel AC\), \(K \in CH\).
6) Следовательно, \(K \in CH\), \(M \in KH\), \(K \in CM\). Доказательство завершено.
Рассмотрим доказательство утверждения, что точка \( K \) лежит на медиане \( CM \) треугольника \( \triangle ABC \).
1. Пусть \( AM = MB = d \), \( AE = FM = f \). По свойству медианы треугольника \( EFK \), точка \( M \) делит отрезок \( EM \) пополам. Следовательно, \( EM = MF = d — f \).
2. Выполним дополнительное построение. Обозначим точки пересечения: \( D = AC \cap FK \), \( G = BC \cap EK \).
3. Рассмотрим четырехугольник \( KGCD \). По построению \( KGCD \) является параллелограммом, так как \( EK \parallel AC \) и \( FK \parallel BC \). Диагональ \( KC \) делит параллелограмм на два равных треугольника. Следовательно, углы \( \angle DCG \) и \( \angle DKG \) равны углу \( \angle C \).
4. Достроим четырехугольник \( AEFK \) до параллелограмма \( EHFK \). В параллелограмме \( EHFK \) точка \( M \) является точкой пересечения диагоналей и делит их пополам. Так как \( M \) находится на прямой \( KH \), то \( KM \) продолжает диагональ параллелограмма.
5. По построению \( HF \parallel AC \). Рассмотрим секущую \( AC \). Точка \( D \) принадлежит прямой \( FK \). Угол между прямыми \( AC \) и \( FK \) обозначим как \( \angle ACH \). Этот угол равен углу \( \angle HFD \), так как \( HF \parallel AC \). Угол \( \angle HFD \) равен углу \( \angle HFK \) по свойству параллелограмма. Таким образом, \( \angle ACH = \angle HFK \).
6. Рассмотрим секущую \( EK \). Угол между прямыми \( EK \) и \( CH \) обозначим как \( \angle EKH \). Этот угол равен углу \( \angle CHFK \), так как \( EK \parallel AC \). Следовательно, \( \angle ACH = \angle EKH \).
7. Из вышеизложенного следует, что точка \( K \) лежит на прямой \( CH \). Так как точка \( M \) лежит на прямой \( KH \), то точка \( K \) также принадлежит медиане \( CM \) треугольника \( \triangle ABC \).
Таким образом, доказательство завершено. Точка \( K \) действительно лежит на медиане \( CM \).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.