ГДЗ по Геометрии 9 класс Номер 849 Атанасян — Подробные Ответы

Докажите, что отрезки, соединяющие основания высот остроугольного треугольника, образуют треугольник, в котором эти высоты являются биссектрисами.  

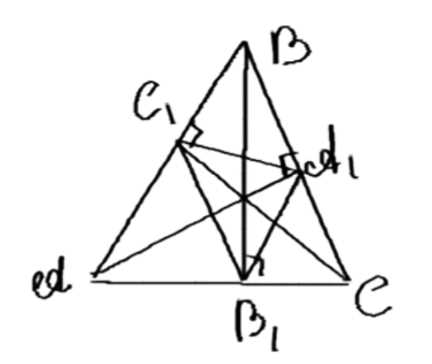
Дано: ΔABC — остроугольный треугольник; AA₁, BB₁, CC₁ — высоты; A₂ = AA₁ ∩ B₁C₁; B₂ = BB₁ ∩ A₁C₁; C₂ = CC₁ ∩ A₁B₁. Доказать, что A₁A₂, B₁B₂, C₁C₂ — биссектрисы треугольника ΔA₁B₁C₁.

Решение:
1. Пересечение всех высот треугольника ABC обозначим точкой M.
2. Запишем выражение для нахождения площади треугольника ABC:
\(S = \frac{1}{2} BC \cdot AA₁ = \frac{1}{2} AC \cdot BB₁\).
Отсюда:
\(BC \cdot AA₁ = AC \cdot BB₁\).
3. Следовательно, отношение:
\(\frac{BC}{B₁A₁} = \frac{AC}{A₁A₁}\).
Угол ∠C общий для треугольников ΔABC и ΔCB₁A₁.
По третьему признаку подобия треугольников имеем:
ΔABC ∼ ΔCB₁A₁.
4. Аналогично:
ΔC₁A₁B₂ ∼ ΔA₁B₁C₂.
По признаку подобия треугольников получаем:
∠B₁A₁C = ∠A, а также ∠MA₁C₂ = 90° − ∠A.
Таким же образом:
ΔAB₁A₁ ∼ ΔABAC.
Отсюда:
∠BA₁C = ∠A, а также ∠MA₁B₂ = 90° − ∠A.

Делаем вывод:
∠MA₁C₂ = ∠MA₁B₂ = 90° − ∠A.
A₁A₂ — биссектриса угла ∠A₁.

Доказательство того, что B₁B₂ и C₁C₂ — биссектрисы, проводится аналогично.

Дано: ΔABC — остроугольный треугольник, AA₁, BB₁, CC₁ — его высоты, точки пересечения высот обозначим как M. Точки A₂, B₂ и C₂ определяются следующим образом: A₂ = AA₁ ∩ B₁C₁, B₂ = BB₁ ∩ A₁C₁, C₂ = CC₁ ∩ A₁B₁. Требуется доказать, что A₁A₂, B₁B₂ и C₁C₂ являются биссектрисами треугольника ΔA₁B₁C₁.

Решение:

1. Начнем с вычисления площади треугольника ΔABC. Площадь можно выразить двумя способами через высоты:
\( S = \frac{1}{2} BC \cdot AA₁ = \frac{1}{2} AC \cdot BB₁ \).
Отсюда следует равенство:
\( BC \cdot AA₁ = AC \cdot BB₁ \).

2. Рассмотрим отношение сторон:
\(\frac{BC}{B₁A₁} = \frac{AC}{A₁A₁}\).
Угол ∠C общий для треугольников ΔABC и ΔCB₁A₁. По третьему признаку подобия треугольников имеем:
ΔABC ∼ ΔCB₁A₁.

3. Аналогично рассмотрим треугольник ΔC₁A₁B₂ и треугольник ΔA₁B₁C₂. По признаку подобия треугольников получаем:
∠B₁A₁C = ∠A, а также ∠MA₁C₂ = 90° − ∠A.
Таким же образом:
ΔAB₁A₁ ∼ ΔABAC.
Отсюда:
∠BA₁C = ∠A, а также ∠MA₁B₂ = 90° − ∠A.

4. Введем дополнительные обозначения. Пусть A₁A₂ пересекает сторону B₁C₁ в точке A₂. Докажем, что A₁A₂ является биссектрисой угла ∠A₁ треугольника ΔA₁B₁C₁. Для этого рассмотрим треугольники ΔMA₁C₂ и ΔMA₁B₂. Из вышеуказанного подобия следует, что:
∠MA₁C₂ = ∠MA₁B₂ = 90° − ∠A.

5. Делаем вывод: A₁A₂ делит угол ∠A₁ на два равных угла, следовательно, A₁A₂ — биссектриса угла ∠A₁.

6. Аналогично доказывается, что B₁B₂ и C₁C₂ являются биссектрисами углов ∠B₁ и ∠C₁ треугольника ΔA₁B₁C₁. Для этого используются те же свойства подобия треугольников и равенство углов.

Итак, доказательство завершено. A₁A₂, B₁B₂ и C₁C₂ — биссектрисы треугольника ΔA₁B₁C₁.