
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 846 Атанасян — Подробные Ответы
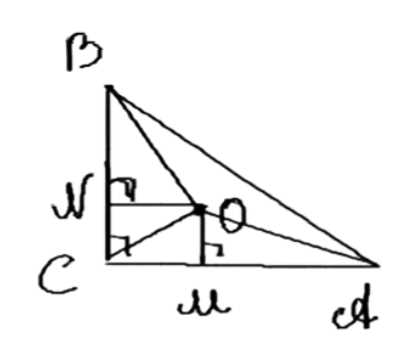
Внутри прямоугольного треугольника \( ABC \) с прямым углом \( C \) взята точка \( O \) так, что справедливо равенство \( S_{OAB} = S_{OAC} = S_{OBC} \). Докажите, что справедливо равенство \( OA^2 + OB^2 = 5OC^2 \).
Рассмотрим задачу, где требуется доказать, что \( OA^2 + OB^2 = 50C^2 \) для прямоугольного треугольника \( \triangle ABC \), в котором \( \angle C = 90^\circ \), площади треугольников \( SOAB = SOAC = SOBC \).
1. Проведем перпендикуляры из точки \( O \) на катеты \( AB \), \( AC \) и \( BC \). Пусть \( OD = p \), \( OE = q \), \( AB = c \), \( AC = b \), \( BC = a \), а площадь треугольника \( \triangle ABC \) равна \( S \). Тогда \( S_{AOB} = S_{AOC} = S_{BOC} = \frac{S}{3} \).
2. Запишем равенства для вычислений:
— \( S_{AOC} = S_{BOC} \), откуда \( \frac{1}{2} bq = \frac{1}{2} ap = \frac{S}{3} \). Следовательно, \( q = \frac{a}{3} \), \( p = \frac{b}{3} \).
— \( CD = q = \frac{a}{3} \), \( BD = a — q = a — \frac{a}{3} = \frac{2a}{3} \).
— \( EC = p = \frac{b}{3} \), \( AE = b — p = b — \frac{b}{3} = \frac{2b}{3} \).
3. Используем теорему Пифагора:
— \( p^2 = OB^2 — BD^2 = OC^2 — CD^2 \), откуда \( \frac{b^2}{9} = OB^2 — \frac{4a^2}{9} = OC^2 — \frac{a^2}{9} \).
— \( q^2 = OC^2 — CE^2 = OA^2 — AE^2 \), откуда \( \frac{a^2}{9} = OC^2 — \frac{b^2}{9} = OA^2 — \frac{4b^2}{9} \).
4. Находим выражения для \( OA^2 \), \( OB^2 \), \( OC^2 \):
— \( OA^2 = \frac{a^2 + 4b^2}{9} \),
— \( OB^2 = \frac{4a^2 + b^2}{9} \),
— \( OC^2 = \frac{a^2 + b^2}{9} \).
5. Складываем \( OA^2 + OB^2 \):
— \( OA^2 + OB^2 = \frac{a^2 + 4b^2}{9} + \frac{4a^2 + b^2}{9} = \frac{5(a^2 + b^2)}{9} \).
6. Учитывая, что \( OC^2 = \frac{a^2 + b^2}{9} \), получаем:
— \( OA^2 + OB^2 = 5 \cdot OC^2 = 50C^2 \), что и требовалось доказать.
Рассмотрим задачу доказательства \( OA^2 + OB^2 = 50C^2 \) для прямоугольного треугольника \( \triangle ABC \), где \( \angle C = 90^\circ \), площади треугольников \( SOAB = SOAC = SOBC \).
1. Пусть \( AB = c \), \( AC = b \), \( BC = a \), а площадь треугольника \( \triangle ABC \) равна \( S = \frac{1}{2} ab \). Из условия \( SOAB = SOAC = SOBC = \frac{S}{3} \).
2. Проведем перпендикуляры \( OD \) и \( OE \) из точки \( O \) на катеты \( AB \) и \( BC \). Пусть \( OD = p \), \( OE = q \). Тогда из равенства площадей:
\(
S_{AOB} = \frac{1}{2} ap = \frac{S}{3}, \quad S_{BOC} = \frac{1}{2} bq = \frac{S}{3}.
\)
Выразим \( p \) и \( q \):
\(
p = \frac{b}{3}, \quad q = \frac{a}{3}.
\)
3. Найдем длины отрезков \( CD \), \( BD \), \( EC \), \( AE \):
\(
CD = q = \frac{a}{3}, \quad BD = a — CD = a — \frac{a}{3} = \frac{2a}{3},
\)
\(
EC = p = \frac{b}{3}, \quad AE = b — EC = b — \frac{b}{3} = \frac{2b}{3}.
\)
4. Используем теорему Пифагора для вычисления \( OA^2 \), \( OB^2 \), \( OC^2 \):
\(
p^2 = OB^2 — BD^2, \quad q^2 = OC^2 — CD^2,
\)
\(
q^2 = OA^2 — AE^2, \quad p^2 = OC^2 — CE^2.
\)
Подставим выражения для \( p \) и \( q \):
\(
p^2 = \left( \frac{b}{3} \right)^2 = \frac{b^2}{9}, \quad q^2 = \left( \frac{a}{3} \right)^2 = \frac{a^2}{9}.
\)
Теперь выразим \( OB^2 \), \( OC^2 \), \( OA^2 \):
\(
OB^2 = BD^2 + p^2 = \left( \frac{2a}{3} \right)^2 + \frac{b^2}{9} = \frac{4a^2}{9} + \frac{b^2}{9} = \frac{4a^2 + b^2}{9},
\)
\(
OC^2 = CD^2 + q^2 = \left( \frac{a}{3} \right)^2 + \frac{b^2}{9} = \frac{a^2}{9} + \frac{b^2}{9} = \frac{a^2 + b^2}{9},
\)
\(
OA^2 = AE^2 + q^2 = \left( \frac{2b}{3} \right)^2 + \frac{a^2}{9} = \frac{4b^2}{9} + \frac{a^2}{9} = \frac{4b^2 + a^2}{9}.
\)
5. Найдем сумму \( OA^2 + OB^2 \):
\(
OA^2 + OB^2 = \frac{4b^2 + a^2}{9} + \frac{4a^2 + b^2}{9} = \frac{4b^2 + a^2 + 4a^2 + b^2}{9} = \frac{5(a^2 + b^2)}{9}.
\)
6. Из условия \( OC^2 = \frac{a^2 + b^2}{9} \), умножим \( OC^2 \) на 5:
\(
5 \cdot OC^2 = 5 \cdot \frac{a^2 + b^2}{9} = \frac{5(a^2 + b^2)}{9}.
\)
Таким образом, \( OA^2 + OB^2 = 5 \cdot OC^2 = 50C^2 \). Доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!