ГДЗ по Геометрии 9 класс Номер 843 Атанасян — Подробные Ответы

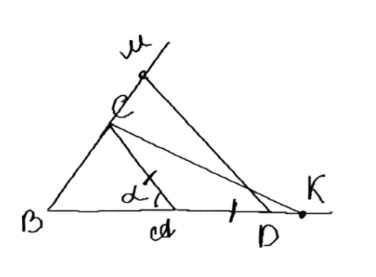
Сторона \( AB \) треугольника \( ABC \) продолжена за точку \( A \) на отрезок \( AD \), равный \( AC \). На лучах \( BA \) и \( BC \) взяты точки \( K \) и \( M \) так, что площади треугольников \( BDM \) и \( BCK \) равны. Найдите угол \( BKM \), если \( \angle BAC = \alpha \).

Дано: треугольник \( \triangle ABC \), \( AD = DC \), \( K \in AB \), \( M \in BC \), \( \angle BAC = \alpha \), площади \( S_{BDM} = S_{BCK} \). Найти угол \( \angle BKM \).

Решение:
1) Углы \( \angle B \) общие, площади \( S_{BDM} = S_{BCK} \). Следовательно,
\[
BD \cdot BM = BK \cdot BC.
\]
Из этого следует пропорция:
\[
\frac{BD}{BK} = \frac{BC}{BM}.
\]
Углы \( \angle B \) общие, значит треугольники \( \triangle BKM \sim \triangle BDC \).

2) Поскольку \( AD = AC \), треугольник \( \triangle ADC \) равнобедренный с основанием \( DC \).
Угол при основании:
\[
\angle ADC = \frac{1}{2} \cdot (180^\circ — \alpha) = \frac{\alpha}{2}.
\]

3) Углы \( \angle BKM = \angle ADC \), так как треугольники \( \triangle BKM \sim \triangle BDC \).
Следовательно,
\[
\angle BKM = \frac{\alpha}{2}.
\]

Ответ: \( \frac{\alpha}{2} \).

Дано: треугольник \( \triangle ABC \), \( AD = DC \), \( K \in AB \), \( M \in BC \), \( \angle BAC = \alpha \), площади \( S_{BDM} = S_{BCK} \). Найти угол \( \angle BKM \).

Решение:

1. Рассмотрим равенство площадей \( S_{BDM} = S_{BCK} \).
Площадь треугольника выражается как половина произведения двух сторон на синус угла между ними. Так как угол \( \angle B \) общий для обоих треугольников, то из равенства площадей следует:
\[
BD \cdot BM = BK \cdot BC.
\]
Это равенство можно переписать в виде пропорции:
\[
\frac{BD}{BK} = \frac{BC}{BM}.
\]
Из этого следует, что треугольники \( \triangle BKM \) и \( \triangle BDC \) подобны, так как у них равны углы \( \angle B \), а их стороны пропорциональны.

2. Поскольку \( AD = AC \), треугольник \( \triangle ADC \) равнобедренный с основанием \( DC \).
В равнобедренном треугольнике угол при основании равен половине разности между \( 180^\circ \) и углом при вершине. Таким образом,
\[
\angle ADC = \frac{1}{2} \cdot (180^\circ — \alpha).
\]
Упростим выражение:
\[
\angle ADC = \frac{\alpha}{2}.
\]

3. Теперь, так как треугольники \( \triangle BKM \) и \( \triangle BDC \) подобны, то соответствующие углы этих треугольников равны. Следовательно, угол \( \angle BKM \) равен углу \( \angle ADC \):
\[
\angle BKM = \angle ADC.
\]
Подставляя значение угла \( \angle ADC \), получаем:
\[
\angle BKM = \frac{\alpha}{2}.
\]

Ответ: \( \frac{\alpha}{2} \).