ГДЗ по Геометрии 9 класс Номер 842 Атанасян — Подробные Ответы

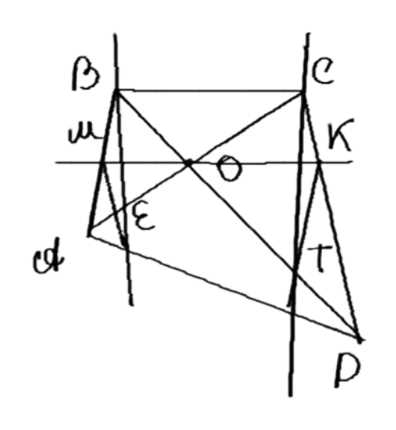
Через точку пересечения диагоналей четырёхугольника \( ABCD \) проведена прямая, пересекающая отрезок \( AB \) в точке \( M \) и отрезок \( CD \) в точке \( K \). Прямая, проведённая через точку \( K \) параллельно отрезку \( AB \), пересекает отрезок \( BD \) в точке \( T \), а прямая, проведённая через точку \( M \) параллельно отрезку \( CD \), пересекает отрезок \( AC \) в точке \( E \). Докажите, что прямые \( BE \) и \( CT \) параллельны.

Дано: четырехугольник \(ABCD\), где \(O = AC \cap BD\), \(K \in CD\), \(M \in AB\), \(T = KT \cap BD\), \(E = ME \cap AC\); \(KT \parallel AB\), \(ME \parallel CD\). Требуется доказать, что \(BE \parallel CT\).

Решение:

1. Рассмотрим треугольники \(KTO\) и \(MBO\):
\(\angle KTO = \angle MBO\) (как вертикальные углы),
\(\angle KTO = \angle MBO\) (как накрест лежащие углы, так как \(KT \parallel AB\)).

Следовательно, треугольники \(KTO\) и \(MBO\) подобны по двум углам:
\[
\triangle KTO \sim \triangle MBO, \quad \frac{KO}{OM} = \frac{KT}{MB}.
\]

2. Рассмотрим треугольники \(KCO\) и \(MEO\):
\(\angle KCO = \angle MEO\) (как вертикальные углы),
\(\angle KCO = \angle MEO\) (как накрест лежащие углы, так как \(ME \parallel CD\)).

Следовательно, треугольники \(KCO\) и \(MEO\) подобны по двум углам:
\[
\triangle KCO \sim \triangle MEO, \quad \frac{KO}{OM} = \frac{KC}{ME}.
\]

Вывод: коэффициенты подобия обеих пар треугольников совпадают.

3. Рассмотрим треугольники \(COT\) и \(EOB\):
\(\triangle COT \sim \triangle EOB\) (по третьему признаку подобия, так как коэффициенты подобия равны, а углы \(\angle COT = \angle EOB\) — вертикальные).

Следовательно, \(\triangle COT \sim \triangle EOB\), а значит, \(BE \parallel CT\).

Доказано.

Дано: четырехугольник \(ABCD\), где \(O = AC \cap BD\), \(K \in CD\), \(M \in AB\), \(T = KT \cap BD\), \(E = ME \cap AC\); \(KT \parallel AB\), \(ME \parallel CD\). Требуется доказать, что \(BE \parallel CT\).

Рассмотрим решение задачи с полной детализацией.

1. Рассмотрим треугольники \(KTO\) и \(MBO\).
Углы \(\angle KTO\) и \(\angle MBO\) равны, так как они вертикальные.
Углы \(\angle KTO\) и \(\angle MBO\) также равны, так как они накрест лежащие при \(KT \parallel AB\) и секущей \(BD\).
Следовательно, треугольники \(KTO\) и \(MBO\) подобны по двум углам.
Коэффициент подобия этих треугольников равен:
\[
\frac{KO}{OM} = \frac{KT}{MB}.
\]

2. Рассмотрим треугольники \(KCO\) и \(MEO\).
Углы \(\angle KCO\) и \(\angle MEO\) равны, так как они вертикальные.
Углы \(\angle KCO\) и \(\angle MEO\) также равны, так как они накрест лежащие при \(ME \parallel CD\) и секущей \(AC\).
Следовательно, треугольники \(KCO\) и \(MEO\) подобны по двум углам.
Коэффициент подобия этих треугольников равен:
\[
\frac{KO}{OM} = \frac{KC}{ME}.
\]

Таким образом, коэффициенты подобия треугольников \(KTO \sim MBO\) и \(KCO \sim MEO\) совпадают.

3. Рассмотрим треугольники \(COT\) и \(EOB\).
Из предыдущих шагов следует, что коэффициенты подобия всех рассмотренных треугольников одинаковы.
Углы \(\angle COT\) и \(\angle EOB\) равны, так как они вертикальные.
Следовательно, треугольники \(COT\) и \(EOB\) подобны по двум углам.
Коэффициент подобия этих треугольников равен:
\[
\frac{CO}{EO} = \frac{CT}{BE}.
\]

Поскольку треугольники \(COT\) и \(EOB\) подобны, а их стороны пропорциональны, прямые \(BE\) и \(CT\) параллельны.

Вывод: \(BE \parallel CT\).
Доказательство завершено.