ГДЗ по Геометрии 9 класс Номер 841 Атанасян — Подробные Ответы

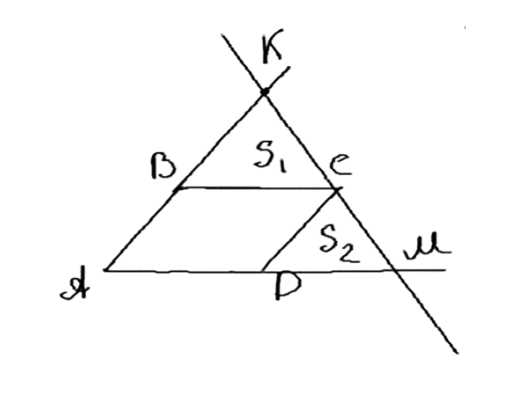
Прямая, проходящая через вершину \( C \) параллелограмма \( ABCD \), пересекает прямые \( AB \) и \( AD \) в точках \( K \) и \( M \). Найдите площадь этого параллелограмма, если площади треугольников \( KBC \) и \( CDM \) равны соответственно \( S_1 \) и \( S_2 \). 

Рассмотрим параллелограмм \(ABCD\), где \(K\) и \(M\) — точки пересечения диагоналей с прямыми \(AB\) и \(AD\) соответственно. Требуется найти площадь \(S_{ABCD}\), если \(S_{KBC} = S_1\) и \(S_{CDM} = S_2\).

1. Рассмотрим треугольники \(AMK\) и \(DMC\). Они подобны по двум углам:
\(\angle AMK = \angle DMC\) (как вертикальные углы),
\(\angle KAM = \angle CDM\) (как накрест лежащие).

Коэффициент подобия треугольников равен:
\(
k = \frac{AM}{MD} = \frac{AK}{DC}.
\)

Отношение площадей подобных треугольников:
\(
\frac{S_{AMK}}{S_{CDM}} = k^2.
\)
Отсюда:
\(
S_{AMK} = k^2 \cdot S_2.
\)

2. Рассмотрим треугольники \(AMK\) и \(KBC\). Они также подобны по двум углам. Коэффициент подобия:
\(
k’ = \frac{KA}{KB} = \frac{KA}{KA + AB}.
\)

Отношение площадей:
\(
\frac{S_{AMK}}{S_{KBC}} = \left(\frac{k}{k+1}\right)^2.
\)
Отсюда:
\(
S_{AMK} = \left(\frac{k}{k+1}\right)^2 \cdot S_1.
\)

3. Запишем уравнение для \(S_{AMK}\):
\(
k^2 \cdot S_2 = \left(\frac{k}{k+1}\right)^2 \cdot S_1.
\)

Раскроем скобки:
\(
k^2 \cdot S_2 = \frac{k^2}{(k+1)^2} \cdot S_1.
\)
Упростим:
\(
(k+1)^2 = \frac{S_1}{S_2}.
\)

Найдем \(k\):
\(
k+1 = \sqrt{\frac{S_1}{S_2}}.
\)
\(
k = \sqrt{\frac{S_1}{S_2}} — 1.
\)

4. Найдем площадь параллелограмма \(S_{ABCD}\):
\(
S_{ABCD} = S_1 — S_{AMK} + S_2.
\)

Подставим \(S_{AMK}\):
\(
S_{ABCD} = S_1 + S_2 — \left(\frac{k^2}{(k+1)^2} \cdot S_1\right).
\)

Подставим значение \(k = \sqrt{\frac{S_1}{S_2}} — 1\):
\(
S_{AMK} = \left(\frac{\sqrt{\frac{S_1}{S_2}} — 1}{\sqrt{\frac{S_1}{S_2}}}\right)^2 \cdot S_1.
\)

Упростим выражение:
\(
S_{ABCD} = S_1 + S_2 — \left(\sqrt{\frac{S_1}{S_2}} — 1\right)^2 \cdot S_2.
\)

Раскрываем скобки:
\(
S_{ABCD} = S_1 + S_2 — \left(\frac{S_1}{S_2} — 2\sqrt{\frac{S_1}{S_2}} + 1\right) \cdot S_2.
\)

Упростим:
\(
S_{ABCD} = S_1 + S_2 — S_1 + 2\sqrt{S_1 S_2} — S_2.
\)

Итоговое выражение:
\(
S_{ABCD} = 2\sqrt{S_1 S_2}.
\)

Ответ:
\(
S_{ABCD} = 2\sqrt{S_1 S_2}.
\)

Рассмотрим параллелограмм \(ABCD\), где \(K\) — точка пересечения прямой \(CK\) с \(AB\), а \(M\) — точка пересечения прямой \(CK\) с \(AD\). Даны площади треугольников \(S_{KBC} = S_1\) и \(S_{CDM} = S_2\). Требуется найти площадь параллелограмма \(S_{ABCD}\).

1. Рассмотрим треугольники \(AMK\) и \(DMC\). Они подобны по двум углам:
\(\angle AMK = \angle DMC\) (как вертикальные углы),
\(\angle KAM = \angle CDM\) (как накрест лежащие).

Следовательно, треугольники \(AMK\) и \(DMC\) подобны. Коэффициент подобия:
\(
k = \frac{AM}{MD} = \frac{AK}{DC}.
\)

Отношение площадей подобных треугольников:
\(
\frac{S_{AMK}}{S_{CDM}} = k^2.
\)
Отсюда:
\(
S_{AMK} = k^2 \cdot S_2.
\)

2. Рассмотрим треугольники \(AMK\) и \(KBC\). Они также подобны по двум углам:
\(\angle AMK = \angle KBC\) (как вертикальные углы),
\(\angle KAM = \angle BKC\) (как накрест лежащие).

Коэффициент подобия:
\(
k’ = \frac{KA}{KB} = \frac{KA}{KA + AB}.
\)

Отношение площадей подобных треугольников:
\(
\frac{S_{AMK}}{S_{KBC}} = \left(\frac{k}{k+1}\right)^2.
\)
Отсюда:
\(
S_{AMK} = \left(\frac{k}{k+1}\right)^2 \cdot S_1.
\)

3. Запишем уравнение для \(S_{AMK}\):
\(
k^2 \cdot S_2 = \left(\frac{k}{k+1}\right)^2 \cdot S_1.
\)

Раскроем скобки:
\(
k^2 \cdot S_2 = \frac{k^2}{(k+1)^2} \cdot S_1.
\)
Упростим:
\(
(k+1)^2 = \frac{S_1}{S_2}.
\)

Найдем \(k\):
\(
k+1 = \sqrt{\frac{S_1}{S_2}}.
\)
\(
k = \sqrt{\frac{S_1}{S_2}} — 1.
\)

4. Найдем площадь параллелограмма \(S_{ABCD}\):
\(
S_{ABCD} = S_1 — S_{AMK} + S_2.
\)

Подставим \(S_{AMK}\):
\(
S_{ABCD} = S_1 + S_2 — \left(\frac{k^2}{(k+1)^2} \cdot S_1\right).
\)

Подставим значение \(k = \sqrt{\frac{S_1}{S_2}} — 1\):
\(
S_{AMK} = \left(\frac{\sqrt{\frac{S_1}{S_2}} — 1}{\sqrt{\frac{S_1}{S_2}}}\right)^2 \cdot S_1.
\)

Упростим выражение:
\(
S_{ABCD} = S_1 + S_2 — \left(\sqrt{\frac{S_1}{S_2}} — 1\right)^2 \cdot S_2.
\)

Раскрываем скобки:
\(
S_{ABCD} = S_1 + S_2 — \left(\frac{S_1}{S_2} — 2\sqrt{\frac{S_1}{S_2}} + 1\right) \cdot S_2.
\)

Упростим:
\(
S_{ABCD} = S_1 + S_2 — S_1 + 2\sqrt{S_1 S_2} — S_2.
\)

Итоговое выражение:
\(
S_{ABCD} = 2\sqrt{S_1 S_2}.
\)

Ответ:
\(
S_{ABCD} = 2\sqrt{S_1 S_2}.
\)