
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 840 Атанасян — Подробные Ответы
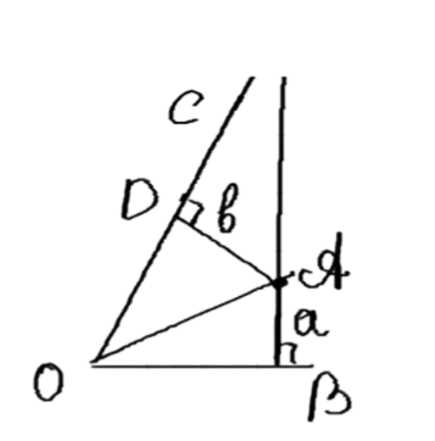
Точка \( A \) лежит внутри угла, равного \( 60^\circ \). Расстояния от точки \( A \) до сторон угла равны \( a \) и \( b \). Найдите расстояние от точки \( A \) до вершины угла.
Дано: \(\angle KOM = 60^\circ\), \(AK \perp KO\), \(AK = a\), \(AM \perp OM\), \(AM = b\). Найти \(AO\).
Решение:
1. Сумма противоположных углов четырехугольника \(OKAM\) равна \(180^\circ\): \(\angle LK + \angle LM = 2 \cdot 90^\circ = 180^\circ\). Следовательно, в четырехугольник можно вписать окружность с диаметром \(AO\).
2. Пусть \(CO = CA = CK = CM = R\).
3. Угол \(\angle KCM = 2 \cdot 60^\circ = 120^\circ\), так как этот угол в два раза больше угла \(KOM\).
4. Треугольник \(KCM\) равнобедренный, его основание \(KM\).
5. Проведем \(CH\), которая будет высотой, биссектрисой и медианой в равнобедренном треугольнике.
6. Рассмотрим треугольник \(\triangle KCH\): \(\angle KHC = 90^\circ\), \(\angle KCH = 60^\circ\), \(CK = R\). Найдем:
\(
KH = CK \cdot \sin 60^\circ = R \cdot \frac{\sqrt{3}}{2}, \quad KM = 2 \cdot KH = R \cdot \sqrt{3}.
\)
7. Угол \(\angle KAM = 360^\circ — 2 \cdot 90^\circ — 60^\circ = 120^\circ\).
8. Рассмотрим треугольник \(\triangle KAM\): \(\angle KAM = 120^\circ\), \(AK = a\), \(AM = b\), \(KM = R \cdot \sqrt{3}\). Используем теорему косинусов:
\(
(R \cdot \sqrt{3})^2 = a^2 + b^2 — 2ab \cdot \cos 120^\circ.
\)
Подставим \(\cos 120^\circ = -\frac{1}{2}\):
\(
3R^2 = a^2 + b^2 — 2ab \cdot \left(-\frac{1}{2}\right) = a^2 + b^2 + ab.
\)
9. Найдем \(R\):
\(
R = \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
10. Диаметр окружности равен \(AO = 2R\):
\(
AO = 2 \cdot \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
Ответ:
\(
AO = 2 \cdot \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
Дано: угол \( \angle KOM = 60^\circ \), \( AK \perp KO \), \( AK = a \), \( AM \perp OM \), \( AM = b \). Найти \( AO \).
Решение:
1. Сумма противоположных углов четырехугольника \( OKAM \) равна \( 180^\circ \):
\(
\angle LK + \angle LM = 2 \cdot 90^\circ = 180^\circ.
\)
Следовательно, в четырехугольник можно вписать окружность, и \( AO \) является диаметром этой окружности.
2. Пусть радиусы окружности равны \( R \), то есть \( CO = CA = CK = CM = R \).
3. Угол \( \angle KCM = 2 \cdot 60^\circ = 120^\circ \), так как этот угол в два раза больше угла \( \angle KOM \).
4. Треугольник \( \triangle KCM \) равнобедренный, его основание \( KM \).
5. Проведем дополнительное построение: высоту \( CH \), которая одновременно является биссектрисой и медианой в равнобедренном треугольнике \( \triangle KCM \).
6. Рассмотрим треугольник \( \triangle KCH \):
Углы треугольника: \( \angle KHC = 90^\circ \), \( \angle KCH = 60^\circ \), а длина стороны \( CK = R \).
Найдем длину \( KH \) по формуле:
\(
KH = CK \cdot \sin 60^\circ = R \cdot \frac{\sqrt{3}}{2}.
\)
Длина основания \( KM \) равна:
\(
KM = 2 \cdot KH = R \cdot \sqrt{3}.
\)
7. Сумма углов четырехугольника равна \( 360^\circ \). Найдем угол \( \angle KAM \):
\(
\angle KAM = 360^\circ — 2 \cdot 90^\circ — 60^\circ = 120^\circ.
\)
8. Рассмотрим треугольник \( \triangle KAM \):
Углы \( \angle KAM = 120^\circ \), \( AK = a \), \( AM = b \), \( KM = R \cdot \sqrt{3} \).
Используем теорему косинусов для нахождения \( KM \):
\(
KM^2 = AK^2 + AM^2 — 2 \cdot AK \cdot AM \cdot \cos \angle KAM.
\)
Подставим значения:
\(
(R \cdot \sqrt{3})^2 = a^2 + b^2 — 2ab \cdot \cos 120^\circ.
\)
Учитывая, что \( \cos 120^\circ = -\frac{1}{2} \), получаем:
\(
3R^2 = a^2 + b^2 — 2ab \cdot \left(-\frac{1}{2}\right) = a^2 + b^2 + ab.
\)
9. Найдем радиус \( R \):
\(
R = \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
10. Диаметр окружности равен \( AO = 2R \):
\(
AO = 2 \cdot \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
Ответ:
\(
AO = 2 \cdot \sqrt{\frac{a^2 + b^2 + ab}{3}}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!