ГДЗ по Геометрии 9 класс Номер 838 Атанасян — Подробные Ответы

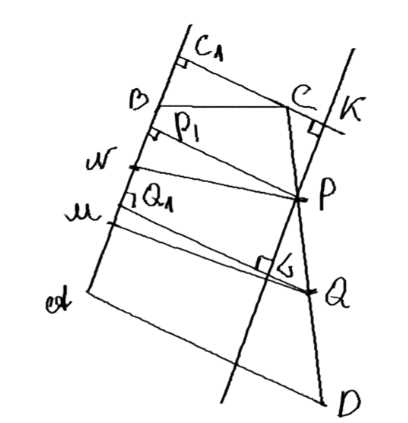
Два непересекающихся отрезка делят каждую из двух противоположных сторон выпуклого четырёхугольника на три равные части. Докажите, что площадь той части четырёхугольника, которая заключена между этими отрезками, в три раза меньше площади самого четырёхугольника.  

Рассмотрим выпуклый четырехугольник \(ABCD\), где \(BE = EF = FC\) и \(AG = GH = HD\). Требуется доказать, что площадь \(S_{EFHG}\) равна трети площади \(S_{ABCD}\).

1. Пусть \(AG = GH = HD = a\), \(BE = EF = FC = b\).

2. Общая площадь четырехугольника \(ABCD\) состоит из двух частей:
\[
S_{ABCD} = (S_{ABG} + S_{GEH} + S_{HFD}) + (S_{BEG} + S_{EFH} + S_{FCD}),
\]
и выражается как:
\[
S_{ABCD} = \frac{a}{2}(DB_1 + DE_1 + DF_1) + \frac{b}{2}(KG_1 + KH_1 + KD_1).
\]

3. Так как \(BE = EF = FC\), то \(B_1E_1 = E_1F_1 = d_1\), следовательно:
\[
DB_1 + DE_1 + DF_1 = (DE_1 — d_1) + DE_1 + (DE_1 + d_1) = 3DE_1.
\]

4. Аналогично:
\[
KG_1 + KH_1 + KD_1 = 3KH_1.
\]

5. Тогда площадь \(S_{ABCD}\) выражается как:
\[
S_{ABCD} = \frac{3}{2}(a \cdot DE_1 + b \cdot KH_1).
\]

6. Найдем площадь среднего четырехугольника \(S_{EFHG}\), который состоит из двух частей:
\[
S_{EFHG} = S_{GEH} + S_{EFH},
\]
и выражается как:
\[
S_{EFHG} = \frac{a}{2}DE_1 + \frac{b}{2}KH_1.
\]

7. Суммарная площадь \(S_{EFHG}\):
\[
S_{EFHG} = \frac{1}{2}(a \cdot DE_1 + b \cdot KH_1).
\]

8. Отношение площадей:
\[
\frac{S_{EFHG}}{S_{ABCD}} = \frac{\frac{1}{2}(a \cdot DE_1 + b \cdot KH_1)}{\frac{3}{2}(a \cdot DE_1 + b \cdot KH_1)} = \frac{1}{3}.
\]

Таким образом, доказано, что:
\[
S_{EFHG} = \frac{1}{3}S_{ABCD}.
\]

Рассмотрим выпуклый четырехугольник \(ABCD\), где \(BE = EF = FC\) и \(AG = GH = HD\). Требуется доказать, что площадь \(S_{EFHG}\) равна трети площади \(S_{ABCD}\).

1. Пусть \(AG = GH = HD = a\), \(BE = EF = FC = b\). Таким образом, стороны четырехугольника делятся на равные части.

2. Общая площадь четырехугольника \(ABCD\) складывается из двух частей: площади треугольников \(ABG\), \(GEH\), \(HFD\) и площади треугольников \(BEG\), \(EFH\), \(FCD\). Тогда:
\[
S_{ABCD} = (S_{ABG} + S_{GEH} + S_{HFD}) + (S_{BEG} + S_{EFH} + S_{FCD}).
\]

3. Площадь каждого треугольника можно выразить через основание и высоту. Для треугольников \(ABG\), \(GEH\), \(HFD\) основание равно \(a\), а высоты \(DB_1\), \(DE_1\), \(DF_1\). Для треугольников \(BEG\), \(EFH\), \(FCD\) основание равно \(b\), а высоты \(KG_1\), \(KH_1\), \(KD_1\).

Таким образом:
\[
S_{ABCD} = \frac{a}{2}(DB_1 + DE_1 + DF_1) + \frac{b}{2}(KG_1 + KH_1 + KD_1).
\]

4. Так как \(BE = EF = FC\), то \(B_1E_1 = E_1F_1 = d_1\). Следовательно:
\[
DB_1 + DE_1 + DF_1 = (DE_1 — d_1) + DE_1 + (DE_1 + d_1).
\]

Упростим:
\[
DB_1 + DE_1 + DF_1 = 3DE_1.
\]

5. Аналогично для треугольников \(BEG\), \(EFH\), \(FCD\):
\[
KG_1 + KH_1 + KD_1 = 3KH_1.
\]

6. Подставим в выражение для площади \(S_{ABCD}\):
\[
S_{ABCD} = \frac{a}{2} \cdot 3DE_1 + \frac{b}{2} \cdot 3KH_1.
\]

Упростим:
\[
S_{ABCD} = \frac{3}{2}(a \cdot DE_1 + b \cdot KH_1).
\]

7. Теперь найдем площадь среднего четырехугольника \(S_{EFHG}\), который состоит из двух треугольников \(GEH\) и \(EFH\). Для треугольника \(GEH\) основание равно \(a\), а высота \(DE_1\). Для треугольника \(EFH\) основание равно \(b\), а высота \(KH_1\). Тогда:
\[
S_{EFHG} = S_{GEH} + S_{EFH}.
\]

Площадь каждого треугольника:
\[
S_{GEH} = \frac{a}{2}DE_1, \quad S_{EFH} = \frac{b}{2}KH_1.
\]

Суммарная площадь:
\[
S_{EFHG} = \frac{a}{2}DE_1 + \frac{b}{2}KH_1.
\]

8. Упростим выражение для \(S_{EFHG}\):
\[
S_{EFHG} = \frac{1}{2}(a \cdot DE_1 + b \cdot KH_1).
\]

9. Найдем отношение площадей \(S_{EFHG}\) и \(S_{ABCD}\):
\[
\frac{S_{EFHG}}{S_{ABCD}} = \frac{\frac{1}{2}(a \cdot DE_1 + b \cdot KH_1)}{\frac{3}{2}(a \cdot DE_1 + b \cdot KH_1)}.
\]

Сократим:
\[
\frac{S_{EFHG}}{S_{ABCD}} = \frac{1}{3}.
\]

10. Таким образом, площадь среднего четырехугольника равна трети площади всего четырехугольника:
\[
S_{EFHG} = \frac{1}{3}S_{ABCD}.
\]