ГДЗ по Геометрии 9 класс Номер 837 Атанасян — Подробные Ответы

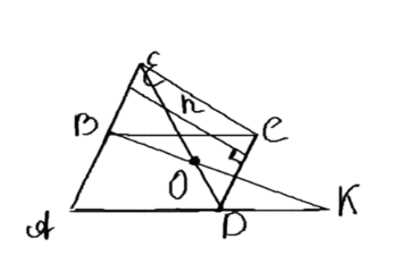
Сторона \( AB \) параллелограмма \( ABCD \) продолжена за точку \( B \) на отрезок \( BE \), а сторона \( AD \) продолжена за точку \( D \) на отрезок \( DK \). Прямые \( ED \) и \( KB \) пересекаются в точке \( O \). Докажите, что площади четырёхугольников \( ABOD \) и \( CEOK \) равны.

Дано: ABCD — параллелограмм; \(DE \parallel AK\); \(B \in AE\); \(O = ED \cap KB\). Требуется доказать, что \(S_{ABOD} = S_{CEOK}\).

Решение:

1. Отметим точки пересечения прямых \(BC\) и \(DE\) точкой \(F\), а пересечение прямых \(KB\) и \(DC\) точкой \(G\).

2. Запишем равенства:
\(
S_{ABOD} = S_{ABD} + S_{BOD} = \frac{1}{2}S_{ABCD} + S_{BOG} — S_{OGD},
\)
\(
S_{CEOK} = S_{CED} — S_{AGD} + S_{CGK} = \frac{1}{2}S_{ABCD} + S_{CGK} — S_{OGD}.
\)

3. Выразим \(S_{BOG}\) и \(S_{CGK}\) через площади треугольников:
\(
S_{BOG} = S_{BDK} — S_{DGK}, \quad S_{CGK} = S_{CDK} — S_{DGK}.
\)

4. Так как треугольники \(BDK\) и \(CDK\) имеют одинаковое основание и высоту, их площади равны:
\(
S_{BDK} = S_{CDK}.
\)

5. Следовательно, \(S_{BOG} = S_{CGK}\), а из равенств для \(S_{ABOD}\) и \(S_{CEOK}\) получаем:
\(
S_{ABOD} = S_{CEOK}.
\)

Доказательство завершено.

Рассмотрим параллелограмм \(ABCD\), где \(DE \parallel AK\), точка \(B\) лежит на диагонали \(AE\), а точка \(O\) является точкой пересечения \(ED\) и \(KB\). Требуется доказать, что площади четырехугольников \(ABOD\) и \(CEOK\) равны.

1. Для начала отметим точки пересечения:
— Точка \(F\) — пересечение прямых \(BC\) и \(DE\).
— Точка \(G\) — пересечение прямых \(KB\) и \(DC\).

2. Запишем выражение для площади четырехугольника \(ABOD\):
\(
S_{ABOD} = S_{ABD} + S_{BOD}.
\)
Площадь треугольника \(ABD\) равна половине площади параллелограмма \(ABCD\), так как диагональ делит параллелограмм на два равных треугольника:
\(
S_{ABD} = \frac{1}{2}S_{ABCD}.
\)
Площадь треугольника \(BOD\) можно выразить через площади треугольников \(BOG\) и \(OGD\):
\(
S_{BOD} = S_{BOG} — S_{OGD}.
\)
Тогда:
\(
S_{ABOD} = \frac{1}{2}S_{ABCD} + S_{BOG} — S_{OGD}.
\)

3. Запишем выражение для площади четырехугольника \(CEOK\):
\(
S_{CEOK} = S_{CED} — S_{AGD} + S_{CGK}.
\)
Площадь треугольника \(CED\) также равна половине площади параллелограмма \(ABCD\):
\(
S_{CED} = \frac{1}{2}S_{ABCD}.
\)
Площадь треугольника \(CGK\) можно выразить через площади треугольников \(CDK\) и \(DGK\):
\(
S_{CGK} = S_{CDK} — S_{DGK}.
\)
Тогда:
\(
S_{CEOK} = \frac{1}{2}S_{ABCD} + S_{CGK} — S_{OGD}.
\)

4. Рассмотрим площади треугольников \(BOG\) и \(CGK\):
— Площадь треугольника \(BOG\) равна разности площадей треугольников \(BDK\) и \(DGK\):
\(
S_{BOG} = S_{BDK} — S_{DGK}.
\)
— Площадь треугольника \(CGK\) равна разности площадей треугольников \(CDK\) и \(DGK\):
\(
S_{CGK} = S_{CDK} — S_{DGK}.
\)

5. Заметим, что треугольники \(BDK\) и \(CDK\) имеют одинаковое основание \(DK\) и высоту, проведенную из точки \(D\) к прямой \(BK\) (так как \(ABCD\) — параллелограмм). Следовательно, их площади равны:
\(
S_{BDK} = S_{CDK}.
\)

6. Таким образом, площади треугольников \(BOG\) и \(CGK\) также равны:
\(
S_{BOG} = S_{CGK}.
\)

7. Подставим это равенство в выражения для \(S_{ABOD}\) и \(S_{CEOK}\):
\(
S_{ABOD} = \frac{1}{2}S_{ABCD} + S_{BOG} — S_{OGD},
\)
\(
S_{CEOK} = \frac{1}{2}S_{ABCD} + S_{CGK} — S_{OGD}.
\)

8. Так как \(S_{BOG} = S_{CGK}\), получаем:
\(
S_{ABOD} = S_{CEOK}.
\)

Доказательство завершено.