ГДЗ по Геометрии 9 класс Номер 835 Атанасян — Подробные Ответы

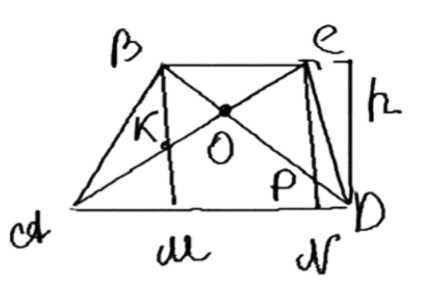
Через концы меньшего основания трапеции проведены две параллельные прямые, пересекающие большее основание. Диагонали трапеции и эти прямые делят трапецию на семь треугольников и один пятиугольник. Докажите, что площадь пятиугольника равна сумме площадей трёх треугольников, прилежащих к боковым сторонам и меньшему основанию трапеции.  

Рассмотрим задачу с трапецией \(ABCD\), где \(AD \parallel BC\), и доказательство того, что \(S_{EGOHF} = S_{ABG} + S_{BCO} + S_{DCH}\).

1. Площади треугольников \(S_{ABC}\) и \(S_{BCD}\) равны:
\(
S_{ABC} = S_{BCD} = \frac{1}{2} BC \cdot h.
\)

2. Сумма площадей треугольников:
\(
S_{ABG} + S_{BGO} + S_{BOC} = S_{DCH} + S_{COH} + S_{BOC}.
\)

3. Площадь фигуры \(EBCF\) равна:
\(
S_{EBCF} = BC \cdot h = 2 \cdot S_{ABC} = S_{ABC} + S_{BCD}.
\)

4. Площадь фигуры \(EGOHF\) равна:
\(
S_{EGOHF} + S_{BGO} + S_{BOC} + S_{COH} = (S_{ABG} + S_{BGO} + S_{BOC}) +\)
\(+ (S_{DCH} + S_{COH} + S_{BOC}).
\)

5. Учитывая вышеуказанные равенства, получаем:
\(
S_{EGOHF} = S_{ABG} + S_{BCO} + S_{DCH}.
\)

Таким образом, доказательство завершено.

Рассмотрим трапецию \(ABCD\), где \(AD \parallel BC\), \(AD > BC\). Даны точки \(E\) и \(F\) на основании \(AD\), \(BE \perp CF\), \(O = AC \cap BD\), \(G = AC \cap BE\), \(H = BD \cap CF\). Требуется доказать, что площадь фигуры \(S_{EGOHF}\) равна сумме площадей \(S_{ABG} + S_{BCO} + S_{DCH}\).

Для доказательства воспользуемся следующим планом:

1. Рассчитаем площади треугольников \(S_{ABC}\) и \(S_{BCD}\). Основание \(BC\) общее для обоих треугольников, высота \(h\) также одинакова. Следовательно:
\(
S_{ABC} = S_{BCD} = \frac{1}{2} BC \cdot h.
\)

2. Рассмотрим сумму площадей треугольников \(S_{ABG}\), \(S_{BGO}\) и \(S_{BOC}\). Она равна сумме площадей треугольников \(S_{DCH}\), \(S_{COH}\) и \(S_{BOC}\):
\(
S_{ABG} + S_{BGO} + S_{BOC} = S_{DCH} + S_{COH} + S_{BOC}.
\)

3. Рассчитаем площадь фигуры \(EBCF\). Площадь этой фигуры равна сумме площадей треугольников \(S_{ABC}\) и \(S_{BCD}\), поскольку \(EBCF\) состоит из двух треугольников, имеющих общее основание \(BC\) и высоту \(h\):
\(
S_{EBCF} = BC \cdot h = 2 \cdot S_{ABC} = S_{ABC} + S_{BCD}.
\)

4. Рассчитаем площадь фигуры \(EGOHF\). Эта фигура состоит из частей, которые можно представить как объединение треугольников. Площадь \(S_{EGOHF}\) включает следующие компоненты:
\(
S_{EGOHF} + S_{BGO} + S_{BOC} + S_{COH} = (S_{ABG} + S_{BGO} + S_{BOC})+\)
\( + (S_{DCH} + S_{COH} + S_{BOC}).
\)

5. Учитывая равенства, приведенные выше, площадь фигуры \(S_{EGOHF}\) выражается как:
\(
S_{EGOHF} = S_{ABG} + S_{BCO} + S_{DCH}.
\)

Таким образом, мы доказали, что площадь фигуры \(S_{EGOHF}\) равна сумме площадей \(S_{ABG}\), \(S_{BCO}\) и \(S_{DCH}\).