
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 833 Атанасян — Подробные Ответы
Докажите, что площадь трапеции равна произведению одной из боковых сторон на перпендикуляр, проведённый из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
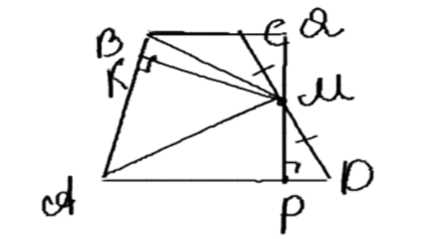
Дано: трапеция \(ABCD\), \(AD \parallel BC\), \(CE = ED\), \(EF \perp AB\), \(F \in AB\). Требуется доказать, что площадь трапеции \(S_{ABCD} = AB \cdot EF\).
Решение:
1. Построим параллелограмм \(ABEK\), где \(EK \parallel AB\) и \(AK \parallel BE\). Его площадь равна \(S_{ABEK} = AB \cdot EF\).
2. Рассмотрим треугольники \(CEM\) и \(DEN\). У них \(CE = DE\), углы \(\angle CEM = \angle DEN\) равны как вертикальные, а \(\angle MCE = \angle NDE\) равны как накрест лежащие (так как \(AD \parallel BC\), \(C\) — секущая). Следовательно, треугольники равны по второму признаку равенства, и их площади совпадают: \(S_{CEM} = S_{DEN}\).
3. Рассмотрим треугольники \(ANK\) и \(BME\). У них \(AK = BE\), углы \(\angle AKN = \angle BEM\) равны как соответствующие, а \(\angle NAK = \angle MBE\) равны (так как \(AK \parallel BE\), \(AD \parallel BC\)). Следовательно, треугольники равны по второму признаку равенства, и их площади совпадают: \(S_{ANK} = S_{BME}\).
4. Выразим площадь трапеции:
\(
S_{ABCD} = S_{ABEN} + S_{BCE} + S_{DEN}.
\)
Подставим:
\(
S_{ABCD} = (S_{ABEK} — S_{ANK}) + (S_{BME} — S_{CEM}) + S_{DEN}.
\)
Учитывая равенства \(S_{CEM} = S_{DEN}\) и \(S_{ANK} = S_{BME}\), получаем:
\(
S_{ABCD} = S_{ABEK}.
\)
Площадь параллелограмма \(ABEK\) равна \(AB \cdot EF\).
Ответ: \(S_{ABCD} = AB \cdot EF\).
Дано: трапеция \(ABCD\), \(AD \parallel BC\), \(CE = ED\), \(EF \perp AB\), \(F \in AB\). Требуется доказать, что площадь трапеции \(S_{ABCD} = AB \cdot EF\).
Решение:
1. Построим параллелограмм \(ABEK\), где \(EK \parallel AB\) и \(AK \parallel BE\). Его площадь равна \(S_{ABEK} = AB \cdot EF\). Это следует из определения площади параллелограмма, которая равна произведению длины основания на высоту, опущенную на основание.
2. Рассмотрим треугольники \(CEM\) и \(DEN\). У них:
— \(CE = DE\) по условию;
— углы \(\angle CEM = \angle DEN\) равны как вертикальные;
— углы \(\angle MCE = \angle NDE\) равны как накрест лежащие (так как \(AD \parallel BC\), \(C\) — секущая).
Следовательно, треугольники \(CEM\) и \(DEN\) равны по второму признаку равенства треугольников (две стороны и угол между ними), и их площади совпадают:
\(
S_{CEM} = S_{DEN}.
\)
3. Рассмотрим треугольники \(ANK\) и \(BME\). У них:
— \(AK = BE\) как противоположные стороны параллелограмма \(ABEK\);
— углы \(\angle AKN = \angle BEM\) равны как соответствующие (так как \(AK \parallel BE\), \(KM\) — секущая);
— углы \(\angle NAK = \angle MBE\) равны как накрест лежащие (так как \(AK \parallel BE\), \(AD \parallel BC\)).
Следовательно, треугольники \(ANK\) и \(BME\) равны по второму признаку равенства треугольников, и их площади совпадают:
\(
S_{ANK} = S_{BME}.
\)
4. Запишем выражение для площади трапеции \(ABCD\):
\(
S_{ABCD} = S_{ABEN} + S_{BCE} + S_{DEN}.
\)
Подставим площади через построенные элементы:
\(
S_{ABCD} = (S_{ABEK} — S_{ANK}) + (S_{BME} — S_{CEM}) + S_{DEN}.
\)
Учитывая равенства \(S_{CEM} = S_{DEN}\) и \(S_{ANK} = S_{BME}\), получаем:
\(
S_{ABCD} = S_{ABEK}.
\)
5. Площадь параллелограмма \(ABEK\) равна произведению основания \(AB\) на высоту \(EF\), опущенную на это основание:
\(
S_{ABEK} = AB \cdot EF.
\)
Таким образом, площадь трапеции \(ABCD\) равна \(AB \cdot EF\), что и требовалось доказать.
Ответ: \(S_{ABCD} = AB \cdot EF\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!