ГДЗ по Геометрии 9 класс Номер 832 Атанасян — Подробные Ответы

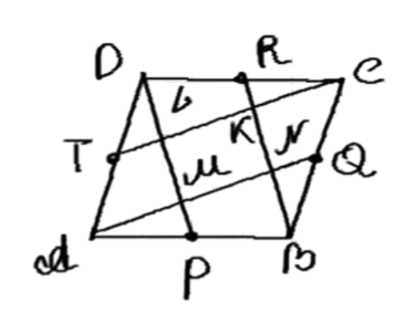
Точки \( P \), \( Q \), \( R \) и \( T \) соответственно — середины сторон \( AB \), \( BC \), \( CD \) и \( DA \) параллелограмма \( ABCD \). Докажите, что при пересечении прямых \( AQ \), \( BR \), \( CT \) и \( DP \) образуется параллелограмм, и найдите отношение его площади к площади параллелограмма \( ABCD \).  

Рассмотрим задачу по шагам:

1. Доказательство параллелограмма EFGH.
Рассмотрим треугольники \( \triangle ABQ \) и \( \triangle CDT \).
\(
AB = CD, \quad BQ = DT = \frac{1}{2} AD, \quad \angle B = \angle D.
\)
По первому признаку равенства треугольников:
\(
\triangle ABQ \cong \triangle CDT.
\)
Следовательно, \( \angle BQA = \angle DTC \).
Далее, \( AD \parallel BC \), \( AQ \) — секущая. Значит, \( \angle BQA = \angle DAQ \) как накрест лежащие.
Отсюда: \( \angle DTC = \angle DAQ \).

Аналогично для треугольников \( \triangle BCR \) и \( \triangle DAP \):
\(
BC = DA, \quad CR = AP = \frac{1}{2} AB, \quad \angle A = \angle C.
\)
По первому признаку равенства треугольников:
\(
\triangle BCR \cong \triangle DAP.
\)
Следовательно, \( \angle APD = \angle ABR \).
Поскольку \( AB \parallel PQ \), то \( BR \parallel PQ \).

В итоге:
\(
AQ \parallel TC, \quad BR \parallel PQ.
\)
Точки \( E, F, G, H \) — пересечения соответствующих прямых. Следовательно, \( EFGH \) — параллелограмм.

2. Найдем отношение площадей.
Рассмотрим треугольники \( \triangle DHT \) и \( \triangle DEA \).
\(
DT = \frac{1}{2} DA, \quad \frac{S_{DHT}}{S_{DEA}} = \frac{1}{4}.
\)
Отсюда:
\(
S_{DEA} = 4 S_{DHT}.
\)
Площадь \( \triangle SAEHT \):
\(
S_{AEHT} = S_{DEA} — S_{DHT} = 3 S_{DHT}.
\)

Найдем площадь \( S_{EFGH} \):
\(
S_{EFGH} = S_{AQCT} — 6 S_{DHT}.
\)
Выразим эту площадь через параллелограмм \( PBRD \):
\(
S_{EFGH} = S_{PBRD} — 6 S_{APE}.
\)
Следовательно:
\(
S_{DHT} = S_{APE}, \quad S_{APD} = S_{APE} + S_{DEA} = S_{DHT} + 4 S_{DHT} = 5 S_{DHT}.
\)
Площадь \( S_{APD} \):
\(
S_{APD} = \frac{1}{5} S_{ABCD}, \quad S_{DHT} = \frac{1}{5} S_{ABCD}.
\)

Находим нужное отношение:
\(
S_{EFGH} = S_{AQCT} — 6 S_{DHT} = 0,2 S_{ABCD}.
\)
Значит:
\(
\frac{S_{EFGH}}{S_{ABCD}} = \frac{1}{5}.
\)

Ответ:
\(
\frac{S_{EFGH}}{S_{ABCD}} = \frac{1}{5}.
\)

Рассмотрим задачу по шагам, подробно разберем каждое утверждение.

1. Доказательство того, что \( EFGH \) — параллелограмм.
Рассмотрим треугольники \( \triangle ABQ \) и \( \triangle CDT \).
Из условия известно:
\( AB = CD \), \( BQ = DT = \frac{1}{2} AD \), \( \angle B = \angle D \).
По первому признаку равенства треугольников:
\(
\triangle ABQ \cong \triangle CDT.
\)
Следовательно, \( \angle BQA = \angle DTC \).
Поскольку \( AD \parallel BC \), а \( AQ \) — секущая, то \( \angle BQA = \angle DAQ \) как накрест лежащие.
Отсюда: \( \angle DTC = \angle DAQ \).

Аналогично рассмотрим треугольники \( \triangle BCR \) и \( \triangle DAP \):
\( BC = DA \), \( CR = AP = \frac{1}{2} AB \), \( \angle A = \angle C \).
По первому признаку равенства треугольников:
\(
\triangle BCR \cong \triangle DAP.
\)
Следовательно, \( \angle APD = \angle ABR \).
Поскольку \( AB \parallel PQ \), то \( BR \parallel PQ \).

В итоге получаем:
\( AQ \parallel TC \), \( BR \parallel PQ \).
Точки \( E, F, G, H \) — пересечения соответствующих прямых. Следовательно, \( EFGH \) — параллелограмм.

2. Найдем отношение площадей \( S_{EFGH} \) и \( S_{ABCD} \).
Рассмотрим треугольники \( \triangle DHT \) и \( \triangle DEA \).
Из условия:
\( DT = \frac{1}{2} DA \).
Так как высота треугольника \( \triangle DHT \) равна половине высоты треугольника \( \triangle DEA \), то их площади связаны соотношением:
\(
\frac{S_{DHT}}{S_{DEA}} = \frac{1}{4}.
\)
Отсюда:
\(
S_{DEA} = 4 S_{DHT}.
\)
Найдем площадь \( \triangle SAEHT \):
\(
S_{AEHT} = S_{DEA} — S_{DHT} = 4 S_{DHT} — S_{DHT} = 3 S_{DHT}.
\)

Теперь найдем площадь \( S_{EFGH} \).
Площадь параллелограмма \( EFGH \) можно выразить как разность площадей:
\(
S_{EFGH} = S_{AQCT} — 6 S_{DHT}.
\)
Выразим эту же площадь через параллелограмм \( PBRD \):
\(
S_{EFGH} = S_{PBRD} — 6 S_{APE}.
\)
Следовательно:
\(
S_{DHT} = S_{APE}.
\)
Площадь \( \triangle APD \):
\(
S_{APD} = S_{APE} + S_{DEA} = S_{DHT} + 4 S_{DHT} = 5 S_{DHT}.
\)
Площадь \( \triangle APD \) выражается через площадь параллелограмма \( ABCD \):
\(
S_{APD} = \frac{1}{5} S_{ABCD}.
\)
Отсюда:
\(
S_{DHT} = \frac{1}{5} S_{ABCD}.
\)

Найдем нужное отношение:
\(
S_{EFGH} = S_{AQCT} — 6 S_{DHT}.
\)
Подставляя значения:
\(
S_{EFGH} = 0,2 S_{ABCD}.
\)
Значит:
\(
\frac{S_{EFGH}}{S_{ABCD}} = \frac{1}{5}.
\)

Ответ:
Отношение площадей \( S_{EFGH} \) и \( S_{ABCD} \) равно \( \frac{1}{5} \).