Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 831 Атанасян — Подробные Ответы
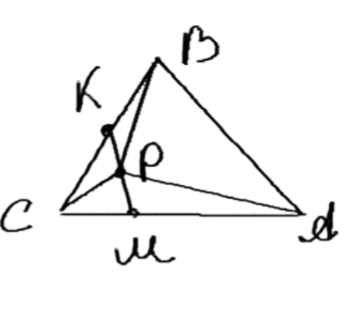
831 На сторонах АС и ВС треугольника АВС взяты точки М и К,
а на отрезке МК — точка Р так, что
\[
\frac{AM}{MC} = \frac{CK}{KB} = \frac{MP}{PK}.
\]
Найдите площадь треугольника АВС, если площади треугольников AMP и BKP равны \( S_1 \) и \( S_2 \).
Рассмотрим задачу по этапам:
1. Пусть \( k = \frac{AM}{MC} = \frac{CK}{KB} = \frac{MP}{PK} \). Тогда площади выражаются следующим образом:
\( S_{AMP} = \frac{S_1}{k}, \, S_{APK} = \frac{S_1}{k} \).
Сумма площадей:
\( S_{AMK} = S_{AMP} + S_{APK} = \left(1 + \frac{1}{k}\right) \cdot S_1 \).
2. Аналогично:
\( S_{KAM} = \frac{S_1}{k}, \, S_{KMC} = \left(1 + \frac{1}{k}\right) \cdot S_1 \).
Сумма площадей:
\( S_{ACK} = S_{KAM} + S_{KMC} = \frac{k+1}{k^2} \cdot S_1 + \frac{k+1}{k^2} \cdot S_1 = \frac{k+1}{k} \cdot S_1 \).
3. Площадь \( S_{AKB} \):
\( S_{AKB} = \frac{1}{k} \cdot \left(\frac{k+1}{k}\right)^2 \cdot S_1 \).
4. Общая площадь \( S_{ABC} \):
\( S_{ABC} = S_{ACK} + S_{AKB} = \frac{(k+1)^3}{k} \cdot S_1 \).
5. С другой стороны:
Пусть \( S_{BMP} = k \cdot S_2, \, S_{BPK} = k \cdot S_2 \). Тогда:
\( S_{BMK} = S_{BMP} + S_{BPK} = (k+1) \cdot S_2 \).
\( S_{MCK} = k \cdot (k+1) \cdot S_2, \, S_{MCB} = (k+1)^2 \cdot S_2 \).
\( S_{BAM} = k \cdot (k+1)^2 \cdot S_2, \, S_{BMC} = k \cdot (k+1)^2 \cdot S_2 \).
Общая площадь:
\( S_{ABC} = S_{BAM} + S_{BMC} = (k+1)^3 \cdot S_2 \).
6. Уравниваем площади:
\( \frac{(k+1)^3}{k} \cdot S_1 = (k+1)^3 \cdot S_2 \).
Отсюда:
\( k^3 = \frac{S_1}{S_2}, \, k = \sqrt[3]{\frac{S_1}{S_2}} \).
7. Подставляем значение \( k \) и находим \( S_{ABC} \):
\( S_{ABC} = (k+1)^3 \cdot S_2 = \left(\sqrt[3]{\frac{S_1}{S_2}} + 1\right)^3 \cdot S_2 \).
Ответ:
\( S_{ABC} = \left(\sqrt[3]{S_1} + \sqrt[3]{S_2}\right)^3 \).
Рассмотрим задачу детально, пошагово.
1. Пусть \( k = \frac{AM}{MC} = \frac{CK}{KB} = \frac{MP}{PK} \). Это соотношение позволяет выразить площади через коэффициент \( k \). Тогда для треугольника \( \triangle AMP \):
\[
S_{AMP} = \frac{S_1}{k}, \quad S_{APK} = \frac{S_1}{k}.
\]
Суммарная площадь треугольника \( \triangle AMK \):
\[
S_{AMK} = S_{AMP} + S_{APK} = \left(1 + \frac{1}{k}\right) \cdot S_1.
\]
2. Аналогично для треугольника \( \triangle KAM \):
\[
S_{KAM} = \frac{S_1}{k}, \quad S_{KMC} = \left(1 + \frac{1}{k}\right) \cdot S_1.
\]
Суммарная площадь треугольника \( \triangle ACK \):
\[
S_{ACK} = S_{KAM} + S_{KMC} = \frac{k+1}{k^2} \cdot S_1 + \frac{k+1}{k^2} \cdot S_1 = \frac{k+1}{k} \cdot S_1.
\]
3. Рассчитаем площадь \( S_{AKB} \), используя пропорцию:
\[
S_{AKB} = \frac{1}{k} \cdot \left(\frac{k+1}{k}\right)^2 \cdot S_1.
\]
Подставляя выражение, получаем:
\[
S_{AKB} = \frac{1}{k} \cdot \frac{(k+1)^2}{k^2} \cdot S_1 = \frac{(k+1)^2}{k^3} \cdot S_1.
\]
4. Общая площадь \( S_{ABC} \) в первой части выражается как сумма:
\[
S_{ABC} = S_{ACK} + S_{AKB}.
\]
Подставим значения:
\[
S_{ABC} = \frac{k+1}{k} \cdot S_1 + \frac{(k+1)^2}{k^3} \cdot S_1 = \frac{(k+1)^3}{k^3} \cdot S_1.
\]
5. Рассмотрим другую сторону задачи. Пусть \( S_{BMP} = k \cdot S_2, \, S_{BPK} = k \cdot S_2 \). Тогда:
\[
S_{BMK} = S_{BMP} + S_{BPK} = (k+1) \cdot S_2.
\]
Рассчитаем площадь \( S_{MCK} \):
\[
S_{MCK} = k \cdot (k+1) \cdot S_2.
\]
Суммарная площадь \( S_{MCB} \):
\[
S_{MCB} = S_{MCK} + S_{BMK} = (k+1)^2 \cdot S_2.
\]
6. Рассчитаем площади \( S_{BAM} \) и \( S_{BMC} \):
\[
S_{BAM} = k \cdot (k+1)^2 \cdot S_2, \quad S_{BMC} = k \cdot (k+1)^2 \cdot S_2.
\]
Общая площадь \( S_{ABC} \):
\[
S_{ABC} = S_{BAM} + S_{BMC} = (k+1)^3 \cdot S_2.
\]
7. Уравниваем выражения для \( S_{ABC} \), полученные двумя способами:
\[
\frac{(k+1)^3}{k^3} \cdot S_1 = (k+1)^3 \cdot S_2.
\]
Сокращаем на \( (k+1)^3 \):
\[
\frac{S_1}{k^3} = S_2.
\]
Отсюда:
\[
k^3 = \frac{S_1}{S_2}, \quad k = \sqrt[3]{\frac{S_1}{S_2}}.
\]
8. Подставляем значение \( k \) в выражение для \( S_{ABC} \):
\[
S_{ABC} = (k+1)^3 \cdot S_2.
\]
Подставим \( k = \sqrt[3]{\frac{S_1}{S_2}} \):
\[
S_{ABC} = \left(\sqrt[3]{\frac{S_1}{S_2}} + 1\right)^3 \cdot S_2.
\]
9. Преобразуем окончательное выражение:
\[
S_{ABC} = \left(\sqrt[3]{S_1} + \sqrt[3]{S_2}\right)^3.
\]
Ответ:
\( S_{ABC} = \left(\sqrt[3]{S_1} + \sqrt[3]{S_2}\right)^3. \)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.