Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 830 Атанасян — Подробные Ответы
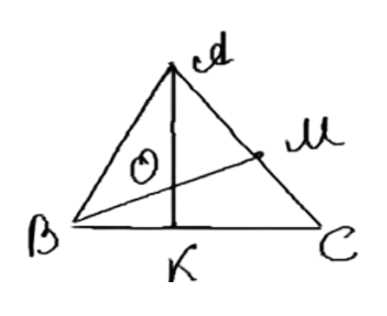
На сторонах \( AC \) и \( BC \) треугольника \( ABC \) взяты соответственно точки \( M \) и \( K \). Отрезки \( AK \) и \( BM \) пересекаются в точке \( O \). Найдите площадь треугольника \( CMK \), если площади треугольников \( OMA \), \( OAB \) и \( OBK \) равны соответственно \( S_1 \), \( S_2 \), \( S_3 \).
Дано: ABCD — параллелограмм; M ∈ AC; M ∈ PR; PR || AD; M ∈ QT; QT || AB; P ∈ AB; Q ∈ BC; R ∈ CD; T ∈ AD.
Требуется доказать: \( S_{MPBQ} = S_{MRDT} \).
Доказательство:
1. Построим перпендикуляры:
\( EF \perp AD \), \( M \in EF \), \( E \in BC \), \( F \in AD \).
\( CH \perp AB \), \( M \in GH \), \( G \in AB \), \( H \in CD \).
2. Обозначим:
\( PB = MQ = a \), \( PM = BQ = b \), \( TM = DR = c \), \( MR = TD = d \),
\( ME = h_1 \), \( MF = h_2 \), \( MG = g_1 \), \( MH = g_2 \).
3. Запишем равенства для нахождения площадей каждого четырехугольника:
\( S_{MPBQ} = BQ \cdot ME = BP \cdot MG \), \( b \cdot h_1 = a \cdot g_1 \).
\( S_{MRDT} = TD \cdot MF = DR \cdot MH \), \( d \cdot h_2 = c \cdot g_2 \).
4. Запишем соотношения:
\( S_{MPBQ} \cdot S_{MPBQ} = b \cdot h_1 \cdot a \cdot g_1 = a \cdot h_1 \cdot b \cdot g_1 = S_{MPBQ} \cdot S_{APMT} \).
\( S_{MRDT} \cdot S_{MRDT} = d \cdot h_2 \cdot c \cdot g_2 = c \cdot g_2 \cdot d \cdot h_2 = S_{MPBQ} \cdot S_{APMT} \).
Отсюда следует, что:
\( S_{MPBQ}^2 = S_{MRDT}^2 \), или \( S_{MPBQ} = S_{MRDT} \).
Что и требовалось доказать.
Дано: ABCD — параллелограмм, M ∈ AC, M ∈ PR, PR || AD, M ∈ QT, QT || AB, P ∈ AB, Q ∈ BC, R ∈ CD, T ∈ AD.
Требуется доказать: \( S_{MPBQ} = S_{MRDT} \).
Доказательство:
1. Построим дополнительные элементы на рисунке:
Проведем перпендикуляры \( EF \perp AD \), \( M \in EF \), \( E \in BC \), \( F \in AD \).
Проведем перпендикуляры \( CH \perp AB \), \( M \in GH \), \( G \in AB \), \( H \in CD \).
Эти перпендикуляры необходимы для вычисления высот и сторон четырехугольников \( MPBQ \) и \( MRDT \).
2. Введем обозначения:
\( PB = MQ = a \), \( PM = BQ = b \), \( TM = DR = c \), \( MR = TD = d \).
Высоты: \( ME = h_1 \), \( MF = h_2 \), \( MG = g_1 \), \( MH = g_2 \).
3. Выражаем площади четырехугольников через их стороны и высоты:
Площадь \( S_{MPBQ} \) вычисляется как:
\[ S_{MPBQ} = BQ \cdot ME = BP \cdot MG \].
Подставляем обозначения: \( b \cdot h_1 = a \cdot g_1 \).
Площадь \( S_{MRDT} \) вычисляется как:
\[ S_{MRDT} = TD \cdot MF = DR \cdot MH \].
Подставляем обозначения: \( d \cdot h_2 = c \cdot g_2 \).
4. Установим равенство произведений сторон и высот:
Запишем равенство для \( S_{MPBQ} \):
\[ S_{MPBQ} \cdot S_{MPBQ} = b \cdot h_1 \cdot a \cdot g_1 = a \cdot h_1 \cdot b \cdot g_1 = S_{MPBQ} \cdot S_{APMT} \].
Запишем равенство для \( S_{MRDT} \):
\[ S_{MRDT} \cdot S_{MRDT} = d \cdot h_2 \cdot c \cdot g_2 = c \cdot g_2 \cdot d \cdot h_2 = S_{MPBQ} \cdot S_{APMT} \].
5. Сравниваем площади:
Так как обе площади \( S_{MPBQ} \) и \( S_{MRDT} \) выражаются через одинаковые произведения, то:
\[ S_{MPBQ}^2 = S_{MRDT}^2 \].
Отсюда следует, что:
\[ S_{MPBQ} = S_{MRDT} \].
Что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.