
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 828 Атанасян — Подробные Ответы
Докажите, что если треугольник имеет:
а) ось симметрии, то он равнобедренный;
б) более чем одну ось симметрии, то он равносторонний.
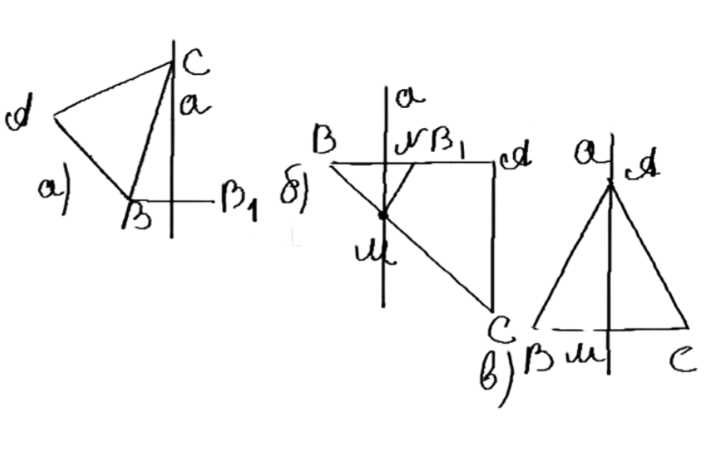
Дано: треугольник \( \triangle ABC \), \( MN \) — ось симметрии. Требуется доказать, что \( \triangle ABC \) равнобедренный.
Рассмотрим два случая:
а) Если треугольник имеет одну ось симметрии \( MN \), то:
1. Ось симметрии должна проходить через вершину треугольника и пересекать противоположную сторону. Если \( MN \) пересекает сторону \( AC \) и проходит через вершину \( B \), то \( MN \) — серединный перпендикуляр к \( AC \).
2. В точке пересечения \( MN \) с \( AC \) (обозначим точку пересечения как \( O \)) выполняется \( AO = OC \), а также \( BO \perp AC \). Следовательно, \( BO \) — медиана и высота, а \( \triangle ABC \) равнобедренный с основанием \( AC \).
б) Если треугольник имеет две оси симметрии, например \( AD \) и \( BE \), то:
1. \( AD \) и \( BE \) — серединные перпендикуляры, проходящие через вершины \( A \) и \( B \).
2. Из симметрии следует, что \( AB = AC \), \( AB = BC \). Таким образом, \( AB = BC = AC \), то есть треугольник равносторонний.
Вывод: если \( \triangle ABC \) имеет одну ось симметрии, то он равнобедренный. Если треугольник имеет две оси симметрии, то он равносторонний.
Дано: треугольник \( \triangle ABC \), \( MN \) — ось симметрии. Требуется доказать, что \( \triangle ABC \) равнобедренный.
Рассмотрим доказательство задачи.
а) Определение оси симметрии: ось симметрии и фигура должны иметь общие точки.
1. Допустим, что \( MN \) пересекает стороны \( \triangle ABC \), но не проходит через вершину. Тогда треугольник преобразуется в невыпуклый многоугольник, что противоречит определению треугольника.
2. Допустим, что \( MN \) проходит через две вершины и содержит одну из сторон. Тогда одна из вершин треугольника не отображается сама в себя, что также противоречит определению симметрии.
3. Следовательно, \( MN \) — ось симметрии, должна проходить через вершину треугольника и пересекать противоположную сторону.
4. Допустим, что \( MN \) проходит через вершину \( B \) и пересекает сторону \( AC \). Тогда:
\( B \to B_1 = B \), \( A \to A_1 = A \), \( C \to C_1 = C \).
5. Так как \( MN \) — серединный перпендикуляр к \( AC \) (по определению осевой симметрии), то отметим точку пересечения \( O \) и получим:
\( BO \perp AC \), \( AO = OC \). Следовательно, \( BO \) — высота и медиана.
Таким образом, \( \triangle ABC \) — равнобедренный с основанием \( AC \).
Что и требовалось доказать.
б) Мы доказали в пункте а), что ось симметрии треугольника проходит через одну из его вершин, и стороны, прилежащие к этой вершине, равны. Следовательно, треугольник равнобедренный.
1. Допустим, что \( \triangle ABC \) имеет не одну, а две оси симметрии, назовем их \( AD \) и \( BE \), которые проходят через вершины \( A \) и \( B \).
2. Получаем:
\( AD \) — серединный перпендикуляр, \( AB = AC \);
\( BE \) — серединный перпендикуляр, \( AB = BC \).
Следовательно, \( AB = BC = AC \), то есть \( \triangle ABC \) — равносторонний.
3. Так как каждая ось симметрии проходит через вершину, то равносторонний треугольник не может иметь более трех осей симметрии.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!