ГДЗ по Геометрии 9 класс Номер 826 Атанасян — Подробные Ответы

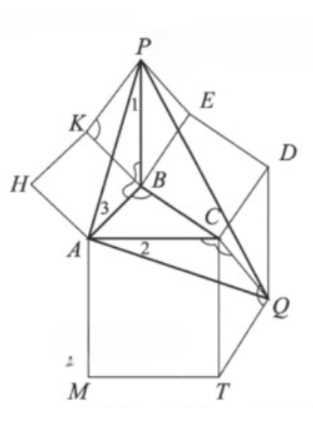
На сторонах треугольника \( ABC \) во внешнюю сторону построены квадраты \( BCDE \), \( ACTM \), \( BAHK \), а затем параллелограммы \( TCDQ \) и \( EBKP \). Докажите, что треугольник \( APQ \) прямоугольный и равнобедренный.  

Дано: \( \triangle ABC \), \( BCDE \), \( ACTM \), \( BAHK \) — квадраты, \( TCPQ \), \( EBKR \) — параллелограммы. Доказать, что \( \triangle APQ \) — прямоугольный и равнобедренный.

Решение:

1. Пусть \( AB = c \), \( BC = a \), \( \angle A = \alpha \), \( \angle B = \beta \).

2. Рассмотрим треугольники \( \triangle ABC \) и \( \triangle QCD \). У них:
\[
AC = TC = QD = b, \quad BC = CD = a.
\]
Угол \( \angle EDQ = \angle BCT = \angle C + 90^\circ \), следовательно, \( \angle CDQ = \angle C \).

По первому признаку равенства треугольников:
\[
\triangle ABC = \triangle QCD, \quad \text{следовательно, } CQ = c.
\]
Угол \( \angle ACQ \) равен:
\[
\angle ACQ = 360^\circ — 90^\circ — (\angle C + \angle B) = 90^\circ + \alpha.
\]

3. Рассмотрим треугольники \( \triangle ABC \) и \( \triangle PEB \). У них:
\[
AB = KB = PE = c, \quad BC = EB = a.
\]
Угол \( \angle PEB \):
\[
\angle PEB = 180^\circ — \angle KBE = 180^\circ — (360^\circ — 290^\circ — \angle B) = \angle B.
\]

По первому признаку равенства треугольников:
\[
\triangle ABC = \triangle PEB, \quad \text{следовательно, } PB = b.
\]
Угол \( \angle PBA \) равен:
\[
\angle PBA = 360^\circ — 90^\circ — (\angle C + \angle B) = 90^\circ + \alpha.
\]

4. Рассмотрим треугольники \( \triangle PBA \) и \( \triangle ACQ \). У них:
\[
\angle PBA = \angle ACQ = 90^\circ + \alpha, \quad BA = CQ = c, \quad PB = AC = b.
\]
По первому признаку равенства треугольников:
\[
\triangle PBA = \triangle ACQ, \quad \text{следовательно, } PA = AQ.
\]
Таким образом, \( \triangle APQ \) равнобедренный с основанием \( PQ \).

5. Пусть \( \angle PBA = \angle CAQ = \gamma \), \( \angle BAP = \angle CQA = \beta \). Сумма углов треугольника:
\[
\gamma + \beta + (90^\circ + \alpha) = 180^\circ, \quad \text{откуда } \gamma + \beta + \alpha = 90^\circ.
\]
Значит, угол при вершине \( \triangle APQ \) прямой:
\[
\angle PAQ = \angle BAP + \angle A + \angle CAQ = \beta + \alpha + \gamma = 90^\circ.
\]

Итак, \( \triangle APQ \) прямоугольный и равнобедренный. Что и требовалось доказать.

Дано: \(\triangle ABC\), \(BCDE\), \(ACTM\), \(BAHK\) — квадраты, \(TCPQ\), \(EBKR\) — параллелограммы. Доказать, что \(\triangle APQ\) — прямоугольный и равнобедренный.

Решение:

1. Пусть \(\overline{AB} = c\), \(\overline{BC} = a\), \(\angle A = \alpha\), \(\angle B = \beta\).

2. Рассмотрим треугольники \(\triangle ABC\) и \(\triangle QCD\). У них:
\[
\overline{AC} = \overline{TC} = \overline{QD} = b, \quad \overline{BC} = \overline{CD} = a.
\]
Угол \(\angle EDQ = \angle BCT = \angle C + 90^\circ\), следовательно:
\[
\angle CDQ = \angle C.
\]

По первому признаку равенства треугольников (\(две стороны и угол между ними\)):
\[
\triangle ABC = \triangle QCD, \quad \text{следовательно, } \overline{CQ} = c.
\]
Угол \(\angle ACQ\) равен:
\[
\angle ACQ = 360^\circ — 90^\circ — (\angle C + \angle B) = 90^\circ + \alpha.
\]

3. Рассмотрим треугольники \(\triangle ABC\) и \(\triangle PEB\). У них:
\[
\overline{AB} = \overline{KB} = \overline{PE} = c, \quad \overline{BC} = \overline{EB} = a.
\]
Угол \(\angle PEB\):
\[
\angle PEB = 180^\circ — \angle KBE = 180^\circ — (360^\circ — 290^\circ — \angle B) = \angle B.
\]

По первому признаку равенства треугольников (\(две стороны и угол между ними\)):
\[
\triangle ABC = \triangle PEB, \quad \text{следовательно, } \overline{PB} = b.
\]
Угол \(\angle PBA\) равен:
\[
\angle PBA = 360^\circ — 90^\circ — (\angle C + \angle B) = 90^\circ + \alpha.
\]

4. Рассмотрим треугольники \(\triangle PBA\) и \(\triangle ACQ\). У них:
\[
\angle PBA = \angle ACQ = 90^\circ + \alpha, \quad \overline{BA} = \overline{CQ} = c, \quad \overline{PB} = \overline{AC} = b.
\]
По первому признаку равенства треугольников (\(две стороны и угол между ними\)):
\[
\triangle PBA = \triangle ACQ, \quad \text{следовательно, } \overline{PA} = \overline{AQ}.
\]
Таким образом, \(\triangle APQ\) равнобедренный с основанием \(\overline{PQ}\).

5. Пусть \(\angle PBA = \angle CAQ = \gamma\), \(\angle BAP = \angle CQA = \beta\). Сумма углов треугольника:
\[
\gamma + \beta + (90^\circ + \alpha) = 180^\circ, \quad \text{откуда } \gamma + \beta + \alpha = 90^\circ.
\]
Значит, угол при вершине \(\triangle APQ\) прямой:
\[
\angle PAQ = \angle BAP + \angle A + \angle CAQ = \beta + \alpha + \gamma = 90^\circ.
\]

Итак, \(\triangle APQ\) прямоугольный и равнобедренный. Что и требовалось доказать.