Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 824 Атанасян — Подробные Ответы
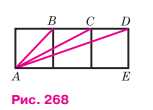
На рисунке 268 изображены три квадрата. Найдите сумму \( \angle BAE + \angle CAE + \angle DAE \).
Рассмотрим задачу. Пусть \( D_1 \) — точка, симметричная точке \( D \) относительно точки \( E \). Тогда \( DD_1 = 2 \cdot DE = FC \), и треугольники \( \triangle AFC \) и \( \triangle ACD_1 \) равны по двум катетам. Следовательно, \( AC = CD_1 \) и \( \angle 1 = \angle 2 \).
Так как \( \angle 2 + \angle 3 = 90^\circ \), то \( \angle 1 + \angle 3 = 90^\circ \). Значит, \( \angle ACD_1 = 180^\circ — (\angle 1 + \angle 3) = 90^\circ \). Таким образом, \( \triangle ACD_1 \) является равнобедренным прямоугольным треугольником с основанием \( AD_1 \), и \( \angle CAD_1 = 45^\circ \).
Треугольники \( \triangle DAE \) и \( \triangle D_1AE \) равны по двум катетам, следовательно, \( \angle DAE = \angle D_1AE \).
Суммируем углы:
\(
\angle BAE + \angle CAE + \angle DAE = 45^\circ + \angle CAE + \angle D_1AE.
\)
Так как \( \angle D_1AE = \angle CAD_1 = 45^\circ \), то:
\(
\angle BAE + \angle CAE + \angle DAE = 45^\circ + 45^\circ = 90^\circ.
\)
Ответ: \( 90^\circ \).
Рассмотрим задачу и разберем решение подробно.
Пусть \( D_1 \) — точка, симметричная точке \( D \) относительно точки \( E \). Тогда \( DD_1 = 2 \cdot DE \), и, следовательно, \( DE = FC \). Также треугольники \( \triangle AFC \) и \( \triangle ACD_1 \) равны по двум катетам (\( AC = CD_1 \) и \( \angle 1 = \angle 2 \)).
Теперь определим угол \( \angle ACD_1 \). Поскольку \( \angle 2 + \angle 3 = 90^\circ \), то \( \angle 1 + \angle 3 = 90^\circ \). Следовательно, угол \( \angle ACD_1 \) можно найти как:
\(
\angle ACD_1 = 180^\circ — (\angle 1 + \angle 3) = 90^\circ.
\)
Таким образом, треугольник \( \triangle ACD_1 \) является равнобедренным прямоугольным треугольником с основанием \( AD_1 \). Это также означает, что:
\(
\angle CAD_1 = 45^\circ.
\)
Рассмотрим треугольники \( \triangle DAE \) и \( \triangle D_1AE \). Они равны по двум катетам (\( AD = AD_1 \) и \( AE \) общая сторона). Следовательно, углы \( \angle DAE \) и \( \angle D_1AE \) равны:
\(
\angle DAE = \angle D_1AE.
\)
Теперь суммируем углы:
\(
\angle BAE + \angle CAE + \angle DAE = 45^\circ + \angle CAE + \angle D_1AE.
\)
Учитывая, что \( \angle D_1AE = \angle CAD_1 = 45^\circ \), получаем:
\(
\angle BAE + \angle CAE + \angle DAE = 45^\circ + 45^\circ = 90^\circ.
\)
Ответ: \( 90^\circ \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.