Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 823 Атанасян — Подробные Ответы
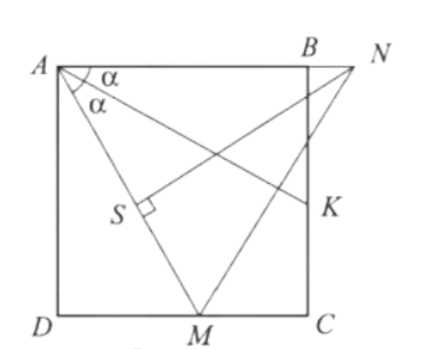
На стороне \( CD \) квадрата \( ABCD \) отмечена точка \( M \). Биссектриса угла \( BAM \) пересекает сторону \( BC \) в точке \( K \). Докажите, что \( AM = BK + DM \).
Рассмотрим задачу.
На луче \( AB \) откладывается отрезок \( AN \), равный отрезку \( AM \). Затем проводится отрезок \( NM \), а также высота \( NS \) в треугольнике \( \triangle AMN \). Пусть угол \( \angle MAK = \angle NAK = \alpha \).
Прямоугольные треугольники \( \triangle ASN \) и \( \triangle MDA \) равны по гипотенузе и острому углу:
\(
AN = AM \text{ (по построению)},\ \angle NAS = 2\alpha,\ \angle AMD = 90^\circ — 2\alpha.
\)
Следовательно, \( \angle NAS = \angle AMD \), отсюда \( AS = DM \) и \( NS = AD \).
Прямоугольные треугольники \( \triangle ABK \) и \( \triangle NSM \) равны по катету и острому углу:
\(
NS = AD = AB,\ \angle BKA = 90^\circ — \alpha,\ \angle SMN = 90^\circ — \alpha.
\)
Таким образом, \( \angle BKA = \angle AMN \), что приводит к равенству \( BK = SM \).
Так как \( BK = SM \) и \( AS = DM \), то:
\(
AM = DM + BK.
\)
Вывод: доказано.
Рассмотрим задачу подробно.
На луче \( AB \) откладывается отрезок \( AN \), равный отрезку \( AM \). Затем проводится отрезок \( NM \), а также высота \( NS \) в треугольнике \( \triangle AMN \). Пусть угол \( \angle MAK = \angle NAK = \alpha \).
1. Рассмотрим треугольники \( \triangle ASN \) и \( \triangle MDA \).
Эти треугольники прямоугольные. В них:
\(
AN = AM \quad \text{(по построению)},
\)
\(
\angle NAS = 2\alpha, \quad \angle AMD = 90^\circ — 2\alpha.
\)
Из условия равенства углов \( \angle NAS = \angle AMD \), можно заключить, что:
\(
AS = DM, \quad NS = AD.
\)
2. Рассмотрим треугольники \( \triangle ABK \) и \( \triangle NSM \).
Эти треугольники также прямоугольные. В них:
\(
NS = AD = AB \quad \text{(по построению)},
\)
\(
\angle BKA = 90^\circ — \alpha, \quad \angle SMN = 90^\circ — \alpha.
\)
Таким образом, углы \( \angle BKA \) и \( \angle AMN \) равны. Следовательно, стороны \( BK \) и \( SM \) также равны:
\(
BK = SM.
\)
3. Теперь можно записать итоговое равенство. Так как:
\(
BK = SM \quad \text{и} \quad AS = DM,
\) то: \(
AM = DM + BK.
\)
Вывод: задача полностью решена, все утверждения доказаны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.