
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 822 Атанасян — Подробные Ответы
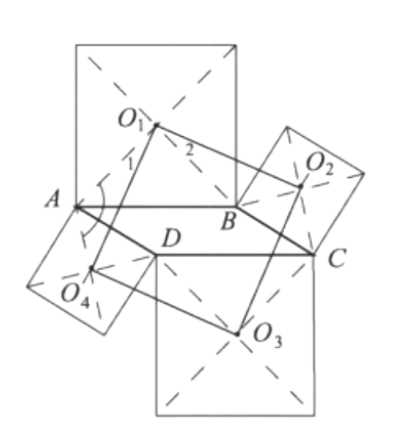
На сторонах параллелограмма вне его построены квадраты. Докажите, что точки пересечения диагоналей этих квадратов являются вершинами квадрата.
Рассмотрим четырехугольник \( O_1O_2O_3O_4 \), где \( O_1, O_2, O_3, O_4 \) — точки пересечения диагоналей квадратов, построенных на сторонах параллелограмма \( ABCD \).
1. Докажем, что треугольники \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \) равны.
У них:
\( AO_1 = BO_1 \) и \( AO_4 = BO_2 \), так как эти отрезки являются половинами диагоналей квадратов.
Углы:
\( \angle AO_1O_4 = 45^\circ + \alpha + 45^\circ = 90^\circ + \alpha \), где \( \alpha = \angle BAD \).
Аналогично:
\( \angle BO_1O_2 = 90^\circ + \alpha \).
Следовательно, треугольники \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \) равны по двум сторонам и углу между ними.
2. Аналогично доказываются равенства для остальных треугольников, из чего следует, что \( O_1O_4 = O_2O_3 \) и \( O_1O_2 = O_3O_4 \).
Таким образом, четырехугольник \( O_1O_2O_3O_4 \) является ромбом.
3. Докажем, что угол \( \angle O_2O_1O_4 \) прямой.
Из равенства треугольников \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \) следует, что \( \angle 1 = \angle 2 \).
Так как \( \angle O_2O_1O_4 = \angle 1 + \angle 2 = 90^\circ \), то ромб \( O_1O_2O_3O_4 \) является квадратом.
Вывод: \( O_1O_2O_3O_4 \) — квадрат.
Рассмотрим четырехугольник \( O_1O_2O_3O_4 \), где \( O_1, O_2, O_3, O_4 \) — точки пересечения диагоналей квадратов, построенных на сторонах параллелограмма \( ABCD \). Требуется доказать, что \( O_1O_2O_3O_4 \) является квадратом.
1. Докажем равенство треугольников \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \).
У этих треугольников:
\( AO_1 = BO_1 \) и \( AO_4 = BO_2 \), так как эти отрезки являются половинами диагоналей квадратов, построенных на сторонах \( AB \) и \( AD \) параллелограмма \( ABCD \).
Углы при вершинах \( O_1 \) и \( O_4 \) равны:
\( \angle AO_1O_4 = 45^\circ + \alpha + 45^\circ = 90^\circ + \alpha \), где \( \alpha = \angle BAD \).
Аналогично:
\( \angle BO_1O_2 = 90^\circ + \alpha \).
Следовательно, треугольники \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \) равны по двум сторонам и углу между ними.
2. Аналогично доказываются равенства для остальных треугольников, из чего следует, что противоположные стороны ромба \( O_1O_2O_3O_4 \) равны:
\( O_1O_4 = O_2O_3 \) и \( O_1O_2 = O_3O_4 \).
Таким образом, четырехугольник \( O_1O_2O_3O_4 \) является ромбом.
3. Докажем, что угол \( \angle O_2O_1O_4 \) прямой.
Рассмотрим равенство треугольников \( \triangle AO_1O_4 \) и \( \triangle BO_1O_2 \).
Из равенства следует, что углы \( \angle 1 \) и \( \angle 2 \) равны.
Так как \( \angle O_2O_1O_4 = \angle 1 + \angle 2 \), а \( \angle 1 + \angle 2 = 90^\circ \), то угол \( \angle O_2O_1O_4 \) прямой.
4. Поскольку ромб с прямым углом является квадратом, то \( O_1O_2O_3O_4 \) является квадратом.
Вывод: \( O_1O_2O_3O_4 \) — квадрат.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!