
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 821 Атанасян — Подробные Ответы
При пересечении биссектрис всех углов прямоугольника образовался четырёхугольник. Докажите, что этот четырёхугольник — квадрат.
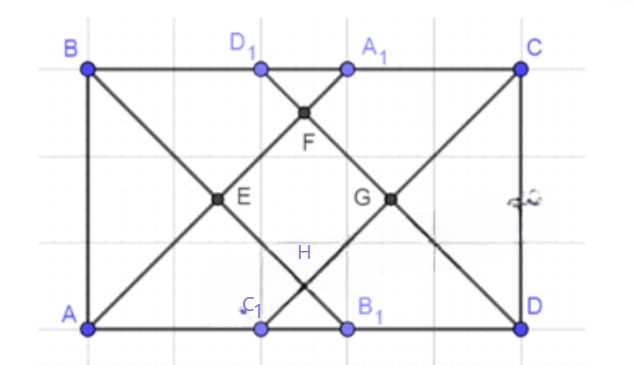
Дано: ABCD — прямоугольник; AA₁, BB₁, CC₁, DD₁ — биссектрисы углов; E = AA₁ ∩ BB₁, F = AA₁ ∩ DD₁, G = CC₁ ∩ DD₁, H = BB₁ ∩ CC₁.
Доказать: EFGH — квадрат.
Решение:
1. В треугольнике AFD биссектрисы углов образуют с его сторонами углы по 45°. Следовательно, ∠FAD = ∠FDA = 45°, а значит, ∠AFD = 90°.
2. Так как AA₁ || CC₁ и BB₁ || DD₁, то четырехугольник EFGH является параллелограммом. Его противоположные стороны равны: EF = HG, FG = EH. Углы при вершинах E и G равны 90° (по свойству биссектрис прямых углов). Следовательно, EFGH — прямоугольник.
3. Для доказательства равенства смежных сторон EF и FG рассмотрим треугольник AFD. В нем AF = FD, так как биссектрисы делят прямой угол пополам.
Треугольники ΔAEB₁ и ΔC₁GD равны по гипотенузе и углу (AE = EB₁, C₁G = GD). Значит, AE = EB₁ = C₁G = GD.
Из равенств AE = FD и AF = GD следует, что EF = FG.
4. Таким образом, все стороны прямоугольника EFGH равны, а углы прямые. Следовательно, EFGH — квадрат.
Ответ: EFGH — квадрат.
Дано: ABCD — прямоугольник, AA₁, BB₁, CC₁, DD₁ — биссектрисы углов; E = AA₁ ∩ BB₁, F = AA₁ ∩ DD₁, G = CC₁ ∩ DD₁, H = BB₁ ∩ CC₁.
Доказать: EFGH — квадрат.
Решение:
1. Рассмотрим треугольник AFD. Биссектрисы углов прямоугольника ABCD делят прямые углы пополам, образуя углы по 45°. Следовательно, в треугольнике AFD:
∠FAD = ∠FDA = 45°.
Это означает, что угол между биссектрисами AA₁ и DD₁ равен 90°:
∠AFD = 90°.
2. Так как AA₁ || CC₁ (биссектрисы противоположных углов прямоугольника параллельны), а BB₁ || DD₁, то четырехугольник EFGH является параллелограммом (по свойству противоположных сторон, лежащих на параллельных прямых).
В параллелограмме противоположные стороны равны:
EF = HG, FG = EH.
3. Углы при вершинах E и G равны 90°, так как биссектрисы пересекаются под прямым углом. Рассмотрим угол ∠E:
∠E = 180° − ∠F = 90°.
Аналогично:
∠G = 90°.
Следовательно, четырехугольник EFGH является прямоугольником.
4. Теперь докажем, что в прямоугольнике EFGH смежные стороны равны. Рассмотрим треугольник AFD:
AF = FD, так как биссектрисы делят угол пополам, а стороны треугольника равны.
Рассмотрим треугольники ΔAEB₁ и ΔC₁GD. Эти треугольники равны по гипотенузе и углу:
AE = EB₁, C₁G = GD.
Следовательно, AE = EB₁ = C₁G = GD.
Так как AF = FD и AE = GD, получаем:
EF = FG.
5. Таким образом, все стороны прямоугольника EFGH равны, а углы прямые. Следовательно, EFGH является квадратом.
Ответ: EFGH — квадрат.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!