
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 820 Атанасян — Подробные Ответы
Докажите, что прямая, проходящая через середины оснований равнобедренной трапеции, перпендикулярна к основаниям. Сформулируйте и докажите обратное утверждение.
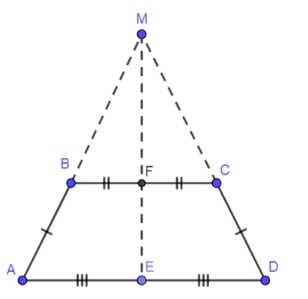
Дано: ABCD — трапеция, AD || BC, AD > BC, AB = CD, E ∈ AD, AE = ED, F ∈ BC, BF = FC.
Доказать: EF ⊥ AD, EF ⊥ BC.
Решение:
1. Продолжим лучи AB и DC до пересечения в точке M.
2. Трапеция равнобедренная, значит ∠A = ∠D. Следовательно, треугольники MBC и MAD равнобедренные.
3. В треугольнике MBC: BF = FC, MF — медиана, так как MB = MC, MF — высота, так как MF ⊥ BC.
4. В треугольнике MAD: AE = ED, ME — медиана, так как MA = MD, ME — высота, так как ME ⊥ AD.
5. Точка F лежит на отрезке ME, так как ME ⊥ AD и ME ⊥ BC. Значит, через точку M можно провести только один перпендикуляр к AD.
Ответ: EF ⊥ AD, EF ⊥ BC.
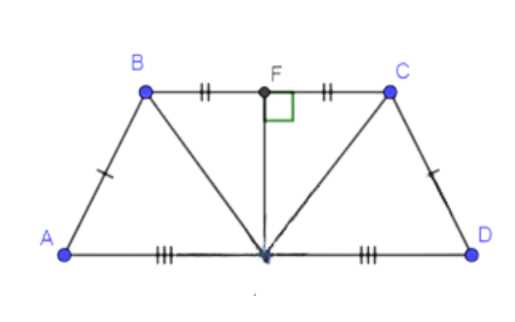
Дано: ABCD — трапеция, AD || BC, AD > BC, E ∈ AD, EF ⊥ AD, AE = ED, F ∈ BC, EF ⊥ BC, BF = FC.
Доказать: AB = CD.
Решение:
1. В треугольнике BEC: BF = FC, EF — медиана, EF ⊥ BC, EF — высота. Следовательно, треугольник BEC равнобедренный, основание BC. Значит, BE = EC, ∠BEF = ∠CEF, ED ⊥ AD, ∠BEA = ∠CED.
2. В треугольниках BEA и CED: AE = ED, BE = EC, ∠BEA = ∠CED. По первому признаку равенства треугольников получаем: △BEA = △CED.
Ответ: AB = CD.
Дано: ABCD — трапеция, AD || BC, AD > BC, AB = CD, E ∈ AD, AE = ED, F ∈ BC, BF = FC.
Доказать: EF ⊥ AD, EF ⊥ BC.
Решение:
1. Продлим лучи AB и DC до пересечения в точке M.
2. Трапеция равнобедренная, следовательно, углы при основании равны: ∠A = ∠D. Это означает, что треугольники MBC и MAD равнобедренные.
В треугольнике MBC: MB = MC, так как трапеция равнобедренная.
3. Рассмотрим треугольник MBC:
BF = FC, так как F — середина основания BC.
MF — медиана, так как MB = MC.
MF — высота, так как MF ⊥ BC.
Таким образом, MF одновременно является медианой и высотой треугольника MBC.
4. Рассмотрим треугольник MAD:
AE = ED, так как точка E делит боковую сторону AD пополам.
ME — медиана, так как MA = MD.
ME — высота, так как ME ⊥ AD.
Таким образом, ME одновременно является медианой и высотой треугольника MAD.
5. Докажем, что точка F лежит на отрезке ME.
Так как ME ⊥ AD и ME ⊥ BC, то MF и ME лежат на одной прямой.
Следовательно, F ∈ ME.
Через точку M можно провести только один перпендикуляр к AD, а также к BC.
Ответ: EF ⊥ AD, EF ⊥ BC.
Дано: ABCD — трапеция, AD || BC, AD > BC, E ∈ AD, EF ⊥ AD, AE = ED, F ∈ BC, EF ⊥ BC, BF = FC.
Доказать: AB = CD.
Решение:
1. Рассмотрим треугольник BEC:
BF = FC, так как F — середина основания BC.
EF — медиана, так как BF = FC.
EF ⊥ BC, так как EF — высота треугольника BEC.
Таким образом, треугольник BEC равнобедренный, основание BC.
Следовательно: BE = EC, ∠BEF = ∠CEF, ED ⊥ AD, ∠BEA = ∠CED.
2. Рассмотрим треугольники BEA и CED:
AE = ED, так как точка E делит боковую сторону AD пополам.
BE = EC, так как треугольник BEC равнобедренный.
∠BEA = ∠CED, так как углы при основании трапеции равны.
По первому признаку равенства треугольников (две стороны и угол между ними равны) получаем: △BEA = △CED.
Следовательно, AB = CD.
Ответ: AB = CD.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!