ГДЗ по Геометрии 9 класс Номер 819 Атанасян — Подробные Ответы

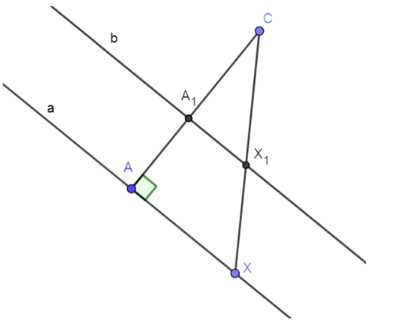
Найдите множество середин всех отрезков, соединяющих данную точку со всеми точками данной прямой, не проходящей через эту точку.  

Дано: \( a \) — прямая; \( C \notin a \).
Найти: множество середин всех отрезков, соединяющих \( C \) со всеми точками прямой \( a \).

Решение:
1. Проведем из точки \( C \) перпендикуляр к прямой \( a \), обозначим точку пересечения как \( A \).
2. Середина отрезка \( AC \) — точка \( A_1 \), где \( A_1A = A_1C = \frac{1}{2}AC \).
3. Через точку \( A_1 \) проведем прямую \( b \), параллельную прямой \( a \).
4. Возьмем произвольную точку \( X \) на прямой \( a \). Середина отрезка \( CX \) обозначается как \( X_1 \).
5. Так как \( A_1X_1 \) — средняя линия треугольника \( ACX \), то \( A_1X_1 \parallel AX \), а значит, \( A_1X_1 \parallel a \).
6. Через точку \( A_1 \), не лежащую на прямой \( a \), можно провести только одну прямую, параллельную \( a \). Следовательно, \( X_1 \in b \).

Ответ: множество середин всех отрезков является прямой, параллельной прямой \( a \), лежащей между точкой \( C \) и прямой \( a \) на половине расстояния между ними.

Дано: \( a \) — прямая; \( C \notin a \).
Найти: множество середин всех отрезков, соединяющих \( C \) со всеми точками прямой \( a \).

Решение:
1. Проведем из точки \( C \) перпендикуляр к прямой \( a \). Обозначим точку пересечения перпендикуляра с прямой \( a \) как \( A \). Точка \( A \) принадлежит прямой \( a \), так как она лежит на пересечении перпендикуляра, проведенного из \( C \), с прямой \( a \).

2. Рассмотрим отрезок \( AC \). Серединой этого отрезка будет точка \( A_1 \), которая делит \( AC \) на две равные части. Таким образом, выполняется условие:
\[
A_1A = A_1C = \frac{1}{2}AC.
\]
Точка \( A_1 \) лежит на перпендикуляре, проведенном из \( C \) к прямой \( a \), и находится на равном расстоянии от точек \( A \) и \( C \).

3. Через точку \( A_1 \) проведем прямую \( b \), которая будет параллельна прямой \( a \). Согласно свойству параллельных прямых, прямая \( b \) не пересекает прямую \( a \) и сохраняет постоянное расстояние до неё.

4. Возьмем произвольную точку \( X \) на прямой \( a \). Соединим точки \( C \) и \( X \), образуя отрезок \( CX \). Необходимо доказать, что середина этого отрезка \( X_1 \) лежит на прямой \( b \).

5. Рассмотрим треугольник \( ACX \), образованный точками \( A \), \( C \) и \( X \). Точка \( A_1 \) лежит на средней линии этого треугольника, так как она является серединой отрезка \( AC \), а \( X_1 \), в свою очередь, является серединой отрезка \( CX \). Средняя линия \( A_1X_1 \) треугольника \( ACX \) параллельна стороне \( AX \) треугольника \( ACX \) по свойству средней линии треугольника. Следовательно, выполняется условие:
\[
A_1X_1 \parallel AX, \quad A_1X_1 \parallel a.
\]

6. Известно, что через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной. Таким образом, прямая \( b \), проходящая через точку \( A_1 \) и параллельная прямой \( a \), является единственной прямой, на которой могут лежать все середины отрезков, соединяющих \( C \) с точками прямой \( a \). Следовательно, середина отрезка \( CX \), обозначенная как \( X_1 \), принадлежит прямой \( b \):
\[
X_1 \in b.
\]

Ответ: множество середин всех отрезков, соединяющих точку \( C \) с точками прямой \( a \), является прямой \( b \), параллельной прямой \( a \), лежащей между точкой \( C \) и прямой \( a \) на половине расстояния между ними.