
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 818 Атанасян — Подробные Ответы
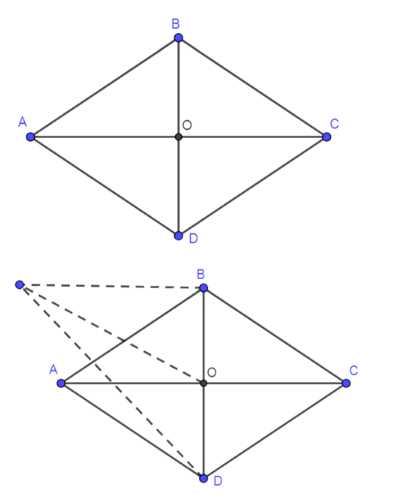
Диагонали выпуклого четырёхугольника разбивают его на четыре треугольника, периметры которых равны. Докажите, что этот четырёхугольник — ромб.
Дано: \( ABCD \) — выпуклый четырехугольник, \( O \) — точка пересечения диагоналей \( AC \) и \( BD \), периметры треугольников равны: \( P_{AOB} = P_{BOC} = P_{COD} = P_{AOD} = P \).
Доказать: \( ABCD \) — ромб.
Решение:
1. По условию равенства периметров треугольников можно записать:
\(
OA + OB + AB = OB + OC + BC, \quad OC + OD + CD = OD + OA +\)
\(+ AD.
\)
Сложив, получаем:
\(
AC + BD + AB + CD = AC + BD + BC + AD.
\)
Отсюда следует:
\(
AB + CD = BC + AD.
\)
2. Суммы противоположных сторон равны, также равны разности смежных сторон:
\(
AB — BC = AD — CD.
\)
3. Предположим, что \( AB > BC \), тогда \( AD > CD \), а \( AO > BO \). Это приводит к противоречию с условием равенства периметров:
\(
P_{AOB} + P_{AOD} > P_{BOC} + P_{COD}.
\)
4. Аналогично, предположим, что \( AB < BC \), тогда снова возникает противоречие:
\(
P_{AOB} + P_{AOD} < P_{BOC} + P_{COD}.
\)
5. Следовательно, \( AB = BC \), \( AD = CD \).
6. Рассмотрим равенство \( AB — AD = BC — CD \). Аналогично предыдущему, получаем:
\(
AB = AD, \quad BC = CD.
\)
Таким образом, \( AB = BC = CD = AD \).
7. По признаку равенства противоположных сторон \( ABCD \) — параллелограмм.
8. Если все стороны параллелограмма равны, то он является ромбом. Следовательно:
\(
ABCD \text{ — ромб.}
\)
Что и требовалось доказать.
Дано: \( ABCD \) — выпуклый четырехугольник, \( O \) — точка пересечения диагоналей \( AC \) и \( BD \), периметры треугольников равны:
\(
P_{AOB} = P_{BOC} = P_{COD} = P_{AOD} = P.
\)
Доказать: \( ABCD \) — ромб.
Решение:
1. Рассмотрим равенство периметров треугольников \( AOB \) и \( BOC \):
\(
OA + OB + AB = OB + OC + BC.
\)
Из этого равенства следует:
\(
OA + AB = OC + BC.
\)
Аналогично для треугольников \( COD \) и \( AOD \):
\(
OC + OD + CD = OD + OA + AD.
\)
Из этого равенства следует:
\(
CD + OC = AD + OA.
\)
Сложим обе пары равенств:
\(
(OA + AB) + (CD + OC) = (OC + BC) + (AD + OA).
\)
Упростим:
\(
AC + BD + AB + CD = AC + BD + BC + AD.
\)
Отсюда получаем:
\(
AB + CD = BC + AD.
\)
2. Суммы противоположных сторон равны, также равны разности смежных сторон. Выразим разности:
\(
AB — BC = AD — CD.
\)
3. Предположим, что \( AB > BC \). Тогда из равенства сумм сторон следует, что \( AD > CD \). Кроме того, из геометрии четырёхугольника следует, что \( AO > BO \). Это приводит к противоречию с условием равенства периметров:
\(
P_{AOB} + P_{AOD} > P_{BOC} + P_{COD}.
\)
Таким образом, предположение \( AB > BC \) неверно.
4. Аналогично предположим, что \( AB < BC \). Тогда из равенства сумм сторон следует, что \( AD < CD \). Кроме того, из геометрии четырёхугольника следует, что \( AO < BO \). Это также приводит к противоречию с условием равенства периметров:
\(
P_{AOB} + P_{AOD} < P_{BOC} + P_{COD}.
\)
Таким образом, предположение \( AB < BC \) неверно.
5. Следовательно, \( AB = BC \), \( AD = CD \).
6. Рассмотрим равенство \( AB — AD = BC — CD \). Подставим равенства \( AB = BC \) и \( AD = CD \):
\(
AB — AD = BC — CD.
\)
Из этого равенства получаем:
\(
AB = AD, \quad BC = CD.
\)
Таким образом, все стороны четырёхугольника равны:
\(
AB = BC = CD = AD.
\)
7. По признаку равенства противоположных сторон \( ABCD \) является параллелограммом.
8. Если все стороны параллелограмма равны, то он является ромбом. Следовательно:
\(
ABCD \text{ — ромб.}
\)
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!