ГДЗ по Геометрии 9 класс Номер 817 Атанасян — Подробные Ответы

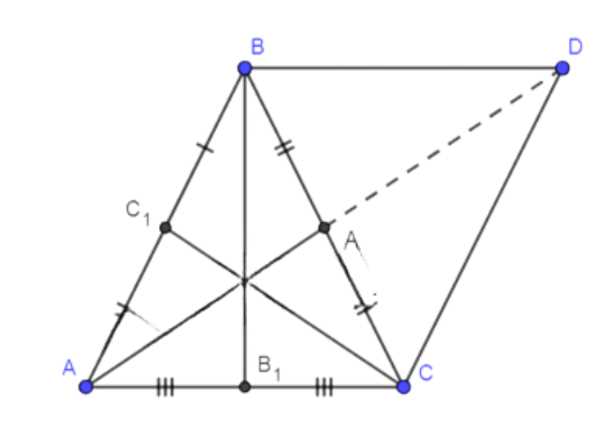
Докажите, что в треугольнике сумма трёх медиан меньше периметра, но больше половины периметра.

Дано: треугольник \( \triangle ABC \), медианы \( AA_1, BB_1, CC_1 \).
Необходимо доказать: \( \frac{P}{2} < AA_1 + BB_1 + CC_1 < P \), где \( P = AB + BC + AC \).

Решение:

1. Рассматриваем параллелограмм \( ABCD \), построенный через продолжение медиан. В нём медианы \( AA_1, BB_1, CC_1 \) равны половине соответствующих диагоналей:
\( AA_1 = \frac{1}{2} AD \), \( BB_1 = \frac{1}{2} BD \), \( CC_1 = \frac{1}{2} CD \).

2. Используем неравенство треугольника для сторон \( AD, BD, CD \):
\( AD < AB + AC \), отсюда \( AA_1 < \frac{AB + AC}{2} \).
Аналогично:
\( BB_1 < \frac{AB + BC}{2} \), \( CC_1 < \frac{AC + BC}{2} \).

3. Складываем полученные неравенства:
\( AA_1 + BB_1 + CC_1 < \frac{AB + AC}{2} + \frac{AB + BC}{2} + \frac{AC + BC}{2} = AB + BC + AC = P \).

4. Рассматриваем треугольники \( ABA_1 \) и \( ACA_1 \), используя неравенство треугольников:
\( AA_1 + A_1B > AB \), \( AA_1 + A_1C > AC \).
Складывая, получаем:
\( 2AA_1 + A_1B + A_1C > AB + AC \), откуда:
\( AA_1 > \frac{AB + AC — BC}{2} \).
Аналогично:
\( BB_1 > \frac{AB + BC — AC}{2} \), \( CC_1 > \frac{AC + BC — AB}{2} \).

5. Складываем три последних неравенства:
\( AA_1 + BB_1 + CC_1 > \frac{AB + AC — BC}{2} + \frac{AB + BC — AC}{2} + \frac{AC + BC — AB}{2} = \)
\( = \frac{AB + BC + AC}{2} = \frac{P}{2} \).

6. Итог:
\( \frac{P}{2} < AA_1 + BB_1 + CC_1 < P \).
Что и требовалось доказать.

Дано: треугольник \( \triangle ABC \), медианы \( AA_1, BB_1, CC_1 \).
Необходимо доказать неравенство:
\(
\frac{P}{2} < AA_1 + BB_1 + CC_1 < P,
\)
где \( P = AB + BC + AC \).

Решение:

1. Рассмотрим параллелограмм \( ABCD \), построенный через продолжение медиан треугольника \( \triangle ABC \).
В данном параллелограмме медианы \( AA_1, BB_1, CC_1 \) равны половине соответствующих диагоналей:
\(
AA_1 = \frac{1}{2}AD, \quad BB_1 = \frac{1}{2}BD, \quad CC_1 = \frac{1}{2}CD.
\)

2. Используем неравенство треугольника для сторон \( AD, BD, CD \) параллелограмма:
\(
AD < AB + AC.
\)
Умножим обе части на \( \frac{1}{2} \):
\(
AA_1 < \frac{AB + AC}{2}.
\)
Аналогично для остальных сторон:
\(
BB_1 < \frac{AB + BC}{2}, \quad CC_1 < \frac{AC + BC}{2}.
\)

3. Складываем полученные неравенства:
\(
AA_1 + BB_1 + CC_1 < \frac{AB + AC}{2} + \frac{AB + BC}{2} + \frac{AC + BC}{2}.
\)
Приведём подобные слагаемые:
\(
AA_1 + BB_1 + CC_1 < AB + BC + AC = P.
\)

4. Рассмотрим треугольники \( ABA_1 \) и \( ACA_1 \), используя неравенство треугольников.
Для треугольника \( ABA_1 \):
\(
AA_1 + A_1B > AB.
\)
Для треугольника \( ACA_1 \):
\(
AA_1 + A_1C > AC.
\)
Складывая эти два неравенства, получаем:
\(
2AA_1 + A_1B + A_1C > AB + AC.
\)
Учитывая, что \( A_1B + A_1C = BC \), имеем:
\(
2AA_1 > AB + AC — BC.
\)
Разделим обе части на \( 2 \):
\(
AA_1 > \frac{AB + AC — BC}{2}.
\)

5. Аналогично для медиан \( BB_1 \) и \( CC_1 \):
Для медианы \( BB_1 \):
\(
BB_1 > \frac{AB + BC — AC}{2}.
\)
Для медианы \( CC_1 \):
\(
CC_1 > \frac{AC + BC — AB}{2}.
\)

6. Складываем три последних неравенства:
\(
AA_1 + BB_1 + CC_1 > \frac{AB + AC — BC}{2} + \frac{AB + BC — AC}{2} + \frac{AC + BC — AB}{2}.
\)
Приведём подобные слагаемые:
\(
AA_1 + BB_1 + CC_1 > \frac{AB + BC + AC}{2} = \frac{P}{2}.
\)

7. Итог:
\(
\frac{P}{2} < AA_1 + BB_1 + CC_1 < P.
\)
Что и требовалось доказать.