ГДЗ по Геометрии 9 класс Номер 816 Атанасян — Подробные Ответы

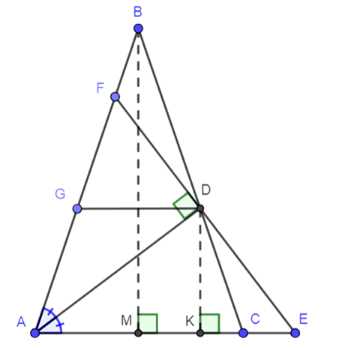
В равнобедренном треугольнике \( ABC \) с основанием \( AC \) проведена биссектриса \( AD \). Прямая, проведённая через точку \( D \) перпендикулярно к \( AD \), пересекает прямую \( AC \) в точке \( E \). Точки \( M \) и \( K \) — основания перпендикуляров, проведённых из точек \( B \) и \( D \) к прямой \( AC \). Найдите \( MK \), если \( AE = a \).

Дано: ΔABC, AB = BC, AD — биссектриса, DE ⊥ AD, E ∈ AC, DK ⊥ AC, K ∈ AC, BM ⊥ AC, M ∈ AC, AE = a.
Найти: MK = ?

Решение:
1) Отметим точку \( F \), где \( F = DE \cap AB \).
2) Рассмотрим треугольник \( FAE \). Поскольку \( AD \) — высота и биссектриса, треугольник \( FAE \) равнобедренный. \( AF = AE = a \), значит, \( AD \) — медиана. Следовательно, \( FD = DE = \frac{1}{2} FE \).
3) Проведем прямую \( GD \), параллельную стороне \( AC \) треугольника. \( G = GD \cap AB \).
4) Так как \( GD \parallel AC \), то \( \triangle FGD \sim \triangle FAE \). Из этого следует:
\(
\frac{CD}{FD} = \frac{AE}{FE}, \quad CD = \frac{1}{2} \cdot AE = \frac{1}{2} \cdot a.
\)
5) Так как \( GD \parallel AC \), то \( \triangle GBD \sim \triangle ABC \). Учитывая, что \( AB = BC \), получаем \( GB = GD \). Следовательно, \( \triangle GBD \) равнобедренный с основанием \( GD \).
6) Отметим точку пересечения \( H = GD \cap BM \). Поскольку \( BM \perp AC \) и \( GD \parallel AC \), то \( BH \perp GD \).
Таким образом, \( BH \) — высота и медиана \( \triangle GBD \), так как \( GB = GD \).
Находим \( GH \):
\(
GH = HD = \frac{1}{2} GD = \frac{1}{2} \cdot \frac{1}{2} a = \frac{1}{4} a.
\)
7) Рассмотрим четырехугольник \( MHDK \). Поскольку \( BM \perp AC \), \( DK \perp AC \), то \( HM \parallel DK \).
Так как \( CD \parallel AC \), то \( HD \parallel MK \).
Следовательно, \( MHDK \) — параллелограмм, а значит, \( MK = HD = \frac{1}{4} a \).

Ответ: \( MK = \frac{1}{4} a \).

Дано: треугольник \( \triangle ABC \), \( AB = BC \), \( AD \) — биссектриса, \( DE \perp AD \), \( E \in AC \), \( DK \perp AC \), \( K \in AC \), \( BM \perp AC \), \( M \in AC \), \( AE = a \).
Найти: \( MK = ? \).

Решение:
1. На стороне \( AB \) отметим точку \( F \), где \( F = DE \cap AB \).
Так как \( DE \perp AD \), то точка \( F \) лежит на стороне \( AB \), а \( FD = DE \).

2. Рассмотрим треугольник \( FAE \).
Треугольник \( FAE \) равнобедренный, так как \( AD \) является одновременно высотой и биссектрисой. Следовательно, \( AF = AE = a \).
Поскольку \( AD \) — медиана, то \( FD = DE = \frac{1}{2} FE \).

3. Проведем прямую \( GD \), параллельную стороне \( AC \) треугольника \( \triangle ABC \). Обозначим точку пересечения \( G = GD \cap AB \).

4. Рассмотрим подобие треугольников \( \triangle FGD \) и \( \triangle FAE \).
Так как \( GD \parallel AC \), то \( \triangle FGD \sim \triangle FAE \). Из подобия следует:
\(
\frac{CD}{FD} = \frac{AE}{FE}.
\)
Подставим значения:
\( AE = a \), \( FD = \frac{1}{2} FE \). Тогда:
\(
CD = \frac{1}{2} \cdot AE = \frac{1}{2} \cdot a = 0,5a.
\)

5. Рассмотрим треугольник \( \triangle GBD \).
Так как \( GD \parallel AC \), то \( \triangle GBD \sim \triangle ABC \). Учитывая, что \( AB = BC \), получаем \( GB = GD \). Следовательно, треугольник \( \triangle GBD \) равнобедренный, основание — \( GD \).

6. Отметим точку пересечения \( H = GD \cap BM \).
Поскольку \( BM \perp AC \) и \( GD \parallel AC \), то \( BH \perp GD \).
Таким образом, \( BH \) является одновременно высотой и медианой треугольника \( \triangle GBD \), так как \( GB = GD \).
Найдем \( GH \):
\(
GH = HD = \frac{1}{2} GD.
\)
А так как \( GD = \frac{1}{2} a \), то:
\(
GH = HD = \frac{1}{2} \cdot \frac{1}{2} a = \frac{1}{4} a.
\)

7. Рассмотрим четырехугольник \( MHDK \).
Поскольку \( BM \perp AC \), \( DK \perp AC \), то \( HM \parallel DK \).
Так как \( CD \parallel AC \), то \( HD \parallel MK \).
Следовательно, \( MHDK \) — параллелограмм.

8. В параллелограмме противоположные стороны равны, поэтому:
\(
MK = HD = \frac{1}{4} a.
\)

Ответ: \( MK = 0,25a \).