
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 814 Атанасян — Подробные Ответы
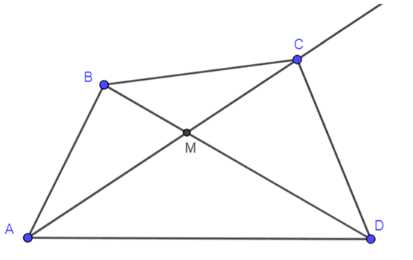
Докажите, что диагонали выпуклого четырёхугольника пересекаются.
Дано: ABCD — выпуклый четырехугольник. Доказать: существует точка \( M = |AC| \cap |BD| \).
Решение:
1. Так как четырехугольник ABCD — выпуклый, то точки \( C \) и \( D \) лежат по одну сторону от прямой \( AB \), а точки \( C \) и \( B \) лежат по одну сторону от прямой \( AD \).
2. Следовательно:
— точка \( C \) находится внутри угла \( \angle BAD \);
— луч \( AC \) — внутри угла \( \angle BAD \);
— луч \( AC \) пересекает любой отрезок с концами на сторонах угла \( \angle BAD \).
Получаем: существует точка \( M = |AC| \cap |BD| \).
3. Теперь рассмотрим прямые \( BA \) и \( BC \). Аналогично предыдущему пункту делаем вывод: \( M = |BD| \cap |AC| \).
Таким образом, точка \( M \) не только лежит на пересечении лучей, но и является точкой пересечения отрезков.
Что и требовалось доказать.
Дано: ABCD — выпуклый четырехугольник.
Необходимо доказать: существует точка \( M = |AC| \cap |BD| \), которая является точкой пересечения диагоналей выпуклого четырехугольника.
Решение:
1. Рассмотрим свойства выпуклого четырехугольника ABCD.
— Выпуклость фигуры означает, что любые две точки внутри четырехугольника можно соединить отрезком, который полностью лежит внутри фигуры.
— Точки \( C \) и \( D \) лежат по одну сторону от прямой \( AB \), поскольку четырехугольник выпуклый.
— Точки \( C \) и \( B \) лежат по одну сторону от прямой \( AD \). Это следует из определения выпуклости.
2. Рассмотрим диагональ \( AC \).
— Точка \( C \) находится внутри угла \( \angle BAD \), так как она лежит внутри четырехугольника.
— Луч \( AC \) также лежит внутри угла \( \angle BAD \), поскольку он соединяет вершины четырехугольника.
— Луч \( AC \) пересекает любой отрезок с концами, лежащими на сторонах угла \( \angle BAD \).
Следовательно, диагональ \( AC \) пересекает диагональ \( BD \) в некоторой точке. Обозначим эту точку как \( M \).
3. Рассмотрим диагональ \( BD \).
— Точки \( B \) и \( D \) лежат по одну сторону от прямой \( AC \), так как четырехугольник выпуклый.
— Луч \( BD \) также лежит внутри угла, образованного прямыми \( BA \) и \( BC \).
— Аналогично предыдущему пункту, диагональ \( BD \) пересекает диагональ \( AC \) в точке \( M \).
4. Таким образом, точка \( M \) является общей точкой для диагоналей \( AC \) и \( BD \), то есть \( M = |AC| \cap |BD| \).
— Точка \( M \) лежит внутри четырехугольника ABCD, так как обе диагонали соединяют противоположные вершины выпуклого четырехугольника.
— Точка \( M \) не только лежит на пересечении лучей \( AC \) и \( BD \), но и является точкой пересечения отрезков \( AC \) и \( BD \).
Ответ: доказано, что существует точка \( M = |AC| \cap |BD| \), которая является точкой пересечения диагоналей выпуклого четырехугольника ABCD.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!