Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 813 Атанасян — Подробные Ответы
Докажите, что из одинаковых плиток, имеющих форму произвольного выпуклого четырёхугольника, можно сделать паркет, полностью покрывающий любую часть плоскости.
Дано: ABCD — выпуклый четырехугольник. Требуется доказать, что с помощью ABCD можно замостить любую часть плоскости.
Решение:
1. Любую плоскость можно замостить треугольниками, из которых легко построить параллелограммы. Параллелограммы, в свою очередь, могут быть использованы для создания полос покрытия.
2. Разделим четырехугольник ABCD на два треугольника. Для этого проведем диагональ, например, AC.
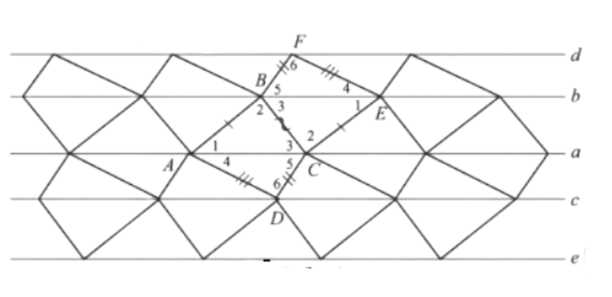
3. К стороне AD прикладываем следующую плитку паркета (стороной A₁D₁). Получается отображение относительно стороны AD, а точка O₁ будет центром симметрии.
4. Повторяем операцию для стороны CD. В итоге формируется полоса из треугольников, равных △ACD.
5. Аналогично продолжаем процесс для других сторон четырехугольника, используя симметрию относительно середины сторон.
6. Каждая полоса состоит из повторяющихся треугольников, что позволяет покрыть всю плоскость без зазоров.
7. Рассмотрим стык четырех плиток в точке пересечения диагоналей. Углы этих плиток примыкают друг к другу:
\[\angle A = \alpha, \, \angle B = \beta, \, \angle C = \gamma, \, \angle D = \delta.\]
Сумма углов равна \(360^\circ\), зазоров не будет.
Вывод: любой выпуклый четырехугольник ABCD может быть использован для покрытия любой части плоскости. Что и требовалось доказать.
Дано: ABCD — выпуклый четырехугольник. Требуется доказать, что с помощью ABCD можно замостить любую часть плоскости.
Решение:
1. Любую плоскость можно замостить треугольниками. Для этого можно использовать метод разбиения плоскости на треугольники, которые затем легко трансформируются в параллелограммы. Параллелограммы, в свою очередь, могут быть использованы для создания полос покрытия.
2. Разделим данный четырехугольник ABCD на два треугольника, проведя одну из диагоналей, например, AC. Таким образом, четырехугольник разделяется на треугольники △ABC и △ACD.
3. Начнем процесс замощения. К стороне AD прикладываем следующую плитку паркета, которая является копией △ACD, отраженной относительно стороны AD. Полученное отображение формирует симметрию относительно стороны AD, а точка O₁ (середина стороны AD) становится центром симметрии.
4. Повторяем аналогичную операцию для стороны CD. При этом к стороне CD прикладывается плитка, которая является копией △ACD, отраженной относительно стороны CD.
5. В результате этих шагов формируется полоса из треугольников, равных △ACD. Углы полосы состоят из зубцов, которые повторяются и равны друг другу.
6. Продолжаем покрывать плоскость. Выбираем центром симметрии точку P₁, которая является серединой стороны BC. Повторяем предыдущие шаги, используя симметрию относительно стороны BC. В итоге получается полоса из треугольников, равных △ABC.
7. Таким образом, за счет составляющих четырехугольник ABCD треугольников образуются полосы, которые можно использовать для покрытия плоскости.
8. Рассмотрим точку пересечения диагоналей четырехугольника ABCD, где сходятся четыре плитки покрытия. Углы этих плиток примыкают друг к другу следующим образом:
\[\angle A = \alpha, \, \angle B = \beta, \, \angle C = \gamma, \, \angle D = \delta.\]
Сумма углов четырехугольника равна
\[\alpha + \beta + \gamma + \delta = 360^\circ.\]
Так как сумма углов равна \(360^\circ\), зазоров между плитками не будет.
Вывод: любой выпуклый четырехугольник ABCD можно использовать для покрытия любой части плоскости. Что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.