Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 812 Атанасян — Подробные Ответы
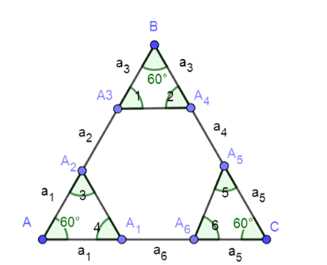
Положительные числа \( a_1, a_2, a_3, a_4, a_5 \) и \( a_6 \) удовлетворяют условиям \( a_1 — a_4 = a_5 — a_2 = a_3 — a_6 \). Докажите, что существует выпуклый шестиугольник \( A_1A_2A_3A_4A_5A_6 \), все углы которого равны, причём \( A_1A_2 = a_1 \), \( A_2A_3 = a_2 \), \( A_5A_4 = a_3 \), \( A_1A_5 = a_4 \), \( A_6A_1 = a_5 \) и \( A_6A_1 = a_6 \).
Дано: выпуклый шестиугольник \( A_1A_2A_3A_4A_5A_6 \), все углы которого равны, и необходимо доказать, что
\( A_1A_2 — A_4A_5 = A_5A_6 — A_2A_3 = A_3A_4 — A_6A_1. \)
Решение:
1. Обозначим длины сторон шестиугольника как \( A_1A_2 = a_1 \), \( A_2A_3 = a_2 \), \( A_3A_4 = a_3 \), \( A_4A_5 = a_4 \), \( A_5A_6 = a_5 \), \( A_6A_1 = a_6 \).
2. Так как все углы равны, то шестиугольник симметричен. Запишем равенства:
\( a_1 — a_4 = a_5 — a_2 = a_3 — a_6. \)
3. Сложим выражения \( a_1 — a_4 \) и \( a_5 — a_2 \):
\( a_1 — a_4 + a_5 — a_2 = a_3 — a_6 + a_3 — a_6. \)
4. Упростим:
\( a_1 + a_5 = a_4 + a_2 + a_3 — a_6. \)
5. Поскольку углы равны, треугольники \( A_1A_2A_3 \), \( A_3A_4A_5 \), \( A_5A_6A_1 \) равнобедренные, а их стороны связаны симметрией. Это приводит к равенству:
\( a_1 — a_4 = a_5 — a_2 = a_3 — a_6. \)
Вывод: доказано, что
\( A_1A_2 — A_4A_5 = A_5A_6 — A_2A_3 = A_3A_4 — A_6A_1. \)
Дано: выпуклый шестиугольник \( A_1A_2A_3A_4A_5A_6 \), все углы которого равны, и необходимо доказать, что
\( A_1A_2 — A_4A_5 = A_5A_6 — A_2A_3 = A_3A_4 — A_6A_1. \)
Решение:
1. Обозначим длины сторон шестиугольника:
\( A_1A_2 = a_1, \, A_2A_3 = a_2, \, A_3A_4 = a_3, \, A_4A_5 = a_4, \, A_5A_6 = a_5, \, A_6A_1 = a_6. \)
2. Так как все углы шестиугольника равны, то он является правильным. Следовательно, его стороны связаны определёнными соотношениями. Запишем равенства:
\( a_1 — a_4 = a_5 — a_2 = a_3 — a_6. \)
3. Рассмотрим равенство \( a_1 — a_4 = a_5 — a_2 \). Добавим к обеим частям выражение \( a_2 + a_3 + a_4 \):
\( a_1 — a_4 + a_2 + a_3 + a_4 = a_5 — a_2 + a_2 + a_3 + a_4. \)
4. Упростим выражение:
\( a_1 + a_2 + a_3 = a_5 + a_3 + a_4. \)
5. Аналогично рассмотрим равенство \( a_5 — a_2 = a_3 — a_6 \). Добавим к обеим частям выражение \( a_6 + a_1 + a_2 \):
\( a_5 — a_2 + a_6 + a_1 + a_2 = a_3 — a_6 + a_6 + a_1 + a_2. \)
6. Упростим выражение:
\( a_5 + a_6 + a_1 = a_3 + a_1 + a_2. \)
7. Теперь рассмотрим равенство \( a_3 — a_6 = a_1 — a_4 \). Добавим к обеим частям выражение \( a_4 + a_5 + a_6 \):
\( a_3 — a_6 + a_4 + a_5 + a_6 = a_1 — a_4 + a_4 + a_5 + a_6. \)
8. Упростим выражение:
\( a_3 + a_4 + a_5 = a_1 + a_5 + a_6. \)
9. Поскольку углы шестиугольника равны, треугольники \( A_1A_2A_3 \), \( A_3A_4A_5 \), \( A_5A_6A_1 \) равнобедренные, а их стороны связаны симметрией. Это приводит к равенству:
\( a_1 — a_4 = a_5 — a_2 = a_3 — a_6. \)
10. Таким образом, доказано, что длины сторон шестиугольника удовлетворяют заданным условиям:
\( A_1A_2 — A_4A_5 = A_5A_6 — A_2A_3 = A_3A_4 — A_6A_1. \)
Ответ: доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.