
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 809 Атанасян — Подробные Ответы
Один из углов прямоугольной трапеции равен \( 120^\circ \). Найдите её среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равны \( a \).
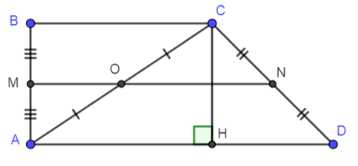
Дано: \(ABCD\) — прямоугольная трапеция, \(\angle A = 90^\circ\), \(\angle C = 120^\circ\), \(AC = a\), \(CD = a\). Найти: \(MN\) — среднюю линию.
Решение:
1. \(AC = CD = a\). Значит, \(\triangle ACD\) — равнобедренный.
2. \(MN\) — средняя линия, следовательно, \(MN \parallel AD\), а \(CN = ND\).
3. По теореме Фалеса:
\(
CO = AO = \frac{AC}{2} = \frac{a}{2}.
\)
4. Углы \(\angle HCD = \angle BCD — \angle BCH = 120^\circ — 90^\circ = 30^\circ\).
5. В равнобедренном \(\triangle ACD\): \(CH\) — высота, биссектриса и медиана. Значит, \(\angle ACH = 30^\circ\), \(AH = HD\).
6. В прямоугольном \(\triangle MAO\), где \(\angle MAO = 30^\circ\):
\(
MO = \frac{1}{2} \cdot AO = \frac{1}{2} \cdot \frac{a}{2} = \frac{a}{4}.
\)
7. В прямоугольном \(\triangle ABC\), где \(\angle BAC = 30^\circ\):
\(
BC = \frac{1}{2} \cdot AC = \frac{a}{2}.
\)
8. Так как \(AH = HD\) и \(AH = BC\), то:
\(
AD = AH + HD = 2 \cdot BC = 2 \cdot \frac{a}{2} = a.
\)
9. \(ON\) — средняя линия, значит:
\(
ON = \frac{1}{2} \cdot AD = \frac{a}{2}.
\)
10. Найдём среднюю линию:
\(
MN = MO + ON = \frac{a}{4} + \frac{a}{2} = \frac{3a}{4}.
\)
Ответ: \(MN = \frac{3a}{4}\).
Дано: \(ABCD\) — прямоугольная трапеция, \(\angle A = 90^\circ\), \(\angle C = 120^\circ\), \(AC = a\), \(CD = a\). Найти: \(MN\) — среднюю линию.
Решение:
1. Так как \(AC = CD = a\), трапеция \(ABCD\) содержит равнобедренный треугольник \(ACD\). Это следует из определения равнобедренного треугольника, у которого две стороны равны.
2. Средняя линия \(MN\) трапеции параллельна её основанию \(AD\), так как по свойствам средней линии она соединяет середины боковых сторон. Следовательно, \(ON \in MN\) и \(ON \parallel AD\).
3. Средняя линия трапеции делит боковые стороны на равные части, то есть \(CN = ND\).
4. Используем теорему Фалеса, так как \(ON \parallel AD\):
\(
CO = AO.
\)
При этом \(CO = AO = \frac{AC}{2} = \frac{a}{2}\).
5. Рассмотрим углы трапеции:
\(
\angle HCD = \angle BCD — \angle BCH = 120^\circ — 90^\circ = 30^\circ.
\)
6. Рассмотрим треугольник \(ACD\): он равнобедренный, поэтому высота \(CH\) является одновременно биссектрисой и медианой. Следовательно,
\(
\angle ACH = \angle HCD = 30^\circ, \, AH = HD.
\)
7. Рассмотрим прямоугольный треугольник \(MAO\), где \(\angle MAO = 30^\circ\). По свойству прямоугольного треугольника с углом \(30^\circ\):
\(
MO = \frac{1}{2} \cdot AO = \frac{1}{2} \cdot \frac{a}{2} = \frac{a}{4}.
\)
8. Рассмотрим прямоугольный треугольник \(ABC\), где \(\angle BAC = 30^\circ\). По свойству прямоугольного треугольника с углом \(30^\circ\):
\(
BC = \frac{1}{2} \cdot AC = \frac{a}{2}.
\)
9. Так как \(AH = HD\) и \(AH = BC\), то:
\(
AD = AH + HD = 2 \cdot BC = 2 \cdot \frac{a}{2} = a.
\)
10. Средняя линия \(ON\) трапеции равна половине её основания \(AD\):
\(
ON = \frac{1}{2} \cdot AD = \frac{a}{2}.
\)
11. Найдём длину средней линии трапеции \(MN\), складывая длины отрезков \(MO\) и \(ON\):
\(
MN = MO + ON = \frac{a}{4} + \frac{a}{2}.
\)
Приведём дроби к общему знаменателю:
\(
MN = \frac{a}{4} + \frac{2a}{4} = \frac{3a}{4}.
\)
Ответ: \(MN = \frac{3a}{4}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!