Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 808 Атанасян — Подробные Ответы
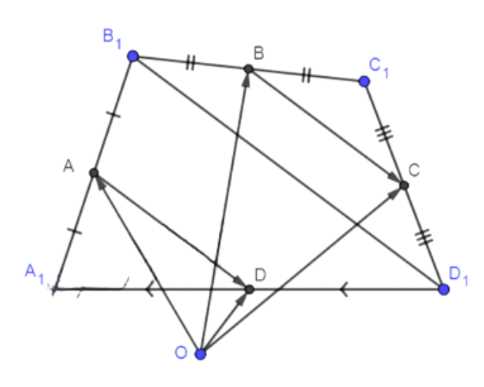
Точки А и С — середины противоположных сторон произвольного четырёхугольника, а точки В и D — середины двух других его сторон. Докажите, что для любой точки О верно равенство
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Дано: \( A_1B_1C_1D_1 \) — произвольный четырёхугольник, \( A, B, C, D \) — середины сторон, \( O \) — произвольная точка. Требуется доказать:
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Решение:
1. Поскольку \( BC \) — средняя линия треугольника \(\Delta B_1C_1D_1\), то:
\[
BC = \frac{1}{2} B_1D_1 \quad \text{и} \quad BC \parallel B_1D_1.
\]
Следовательно:
\[
BB_1 = BC_1, \quad C_1C = CD_1.
\]
2. Аналогично, \( AD \) — средняя линия треугольника \(\Delta A_1B_1D_1\), поэтому:
\[
AD = \frac{1}{2} B_1D_1 \quad \text{и} \quad AD \parallel B_1D_1.
\]
Следовательно:
\[
AA_1 = AB_1, \quad A_1D = DD_1.
\]
3. Из параллельности:
\[
BC \parallel B_1D_1, \quad AD \parallel B_1D_1 \quad \Rightarrow \quad BC \parallel AD.
\]
Так как \( BC = \frac{1}{2} B_1D_1 \) и \( AD = \frac{1}{2} B_1D_1 \), то:
\[
BC = AD.
\]
4. По определению равенства векторов:
\[
\overrightarrow{BC} = \overrightarrow{AD}.
\]
5. Используя свойства векторов:
\[
\overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{BC},
\]
подставляем:
\[
\overrightarrow{BC} = \overrightarrow{OD} — \overrightarrow{OA}.
\]
Тогда:
\[
\overrightarrow{OC} = \overrightarrow{OB} + (\overrightarrow{OD} — \overrightarrow{OA}).
\]
6. Преобразуем:
\[
\overrightarrow{OC} — \overrightarrow{OB} = \overrightarrow{OD} — \overrightarrow{OA}.
\]
Следовательно:
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Ч.т.д.
Дано:
\( A_1B_1C_1D_1 \) — произвольный четырёхугольник, \( A, B, C, D \) — середины сторон, \( O \) — произвольная точка.
Требуется доказать:
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Решение:
1. Рассмотрим треугольник \( \Delta B_1C_1D_1 \).
Отрезок \( BC \) — средняя линия этого треугольника, так как точки \( B \) и \( C \) являются серединами сторон \( B_1C_1 \) и \( C_1D_1 \) соответственно.
По свойству средней линии треугольника:
\[
BC = \frac{1}{2} B_1D_1 \quad \text{и} \quad BC \parallel B_1D_1.
\]
Таким образом, выполняются равенства:
\[
BB_1 = BC_1, \quad C_1C = CD_1.
\]
2. Аналогично рассмотрим треугольник \( \Delta A_1B_1D_1 \).
Отрезок \( AD \) — средняя линия этого треугольника, так как точки \( A \) и \( D \) являются серединами сторон \( A_1B_1 \) и \( B_1D_1 \) соответственно.
По свойству средней линии треугольника:
\[
AD = \frac{1}{2} B_1D_1 \quad \text{и} \quad AD \parallel B_1D_1.
\]
Таким образом, выполняются равенства:
\[
AA_1 = AB_1, \quad A_1D = DD_1.
\]
3. Установим взаимное расположение отрезков \( BC \) и \( AD \).
Поскольку \( BC \parallel B_1D_1 \) и \( AD \parallel B_1D_1 \), то:
\[
BC \parallel AD.
\]
Более того, из равенств:
\[
BC = \frac{1}{2} B_1D_1, \quad AD = \frac{1}{2} B_1D_1,
\]
следует, что:
\[
BC = AD.
\]
4. По определению равенства векторов:
\[
\overrightarrow{BC} = \overrightarrow{AD}.
\]
5. Теперь выразим вектор \( \overrightarrow{OC} \) через \( \overrightarrow{OB} \) и \( \overrightarrow{BC} \):
\[
\overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{BC}.
\]
Подставим вместо \( \overrightarrow{BC} \) его равенство \( \overrightarrow{AD} \):
\[
\overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{AD}.
\]
6. Вектор \( \overrightarrow{AD} \) можно представить как разность векторов \( \overrightarrow{OD} \) и \( \overrightarrow{OA} \):
\[
\overrightarrow{AD} = \overrightarrow{OD} — \overrightarrow{OA}.
\]
Подставим это в выражение для \( \overrightarrow{OC} \):
\[
\overrightarrow{OC} = \overrightarrow{OB} + (\overrightarrow{OD} — \overrightarrow{OA}).
\]
7. Преобразуем выражение:
\[
\overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD} — \overrightarrow{OA}.
\]
Перенесём \( \overrightarrow{OB} \) влево:
\[
\overrightarrow{OC} — \overrightarrow{OB} = \overrightarrow{OD} — \overrightarrow{OA}.
\]
8. Переносим \( \overrightarrow{OA} \) влево и \( \overrightarrow{OB} \) вправо:
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Таким образом, мы доказали требуемое равенство:
\[
\overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{OB} + \overrightarrow{OD}.
\]
Ч.т.д.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.