ГДЗ по Геометрии 9 класс Номер 800 Атанасян — Подробные Ответы

Докажите, что если векторы \( \vec{m} \) и \( \vec{n} \) сонаправлены, то
\( |\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}| \),
а если \( \vec{m} \) и \( \vec{n} \) противоположно направлены, причём \( |\vec{m}| \geq |\vec{n}| \), то
\( |\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}| \).

Рассмотрим векторы \(\vec{m}\) и \(\vec{n}\).

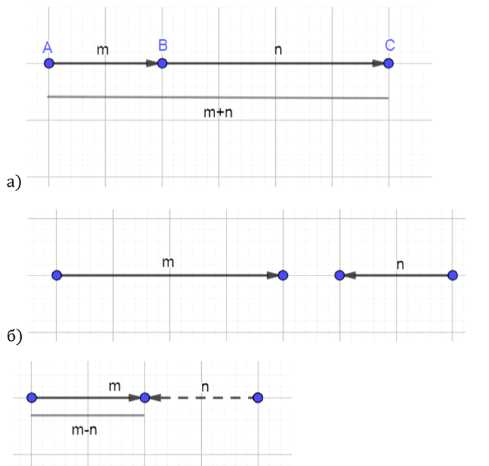
1. Если векторы сонаправлены, то их геометрическая сумма равна:
\(
|\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}|.
\)
В этом случае длина результирующего вектора равна сумме длин исходных векторов.

2. Если векторы противоположно направлены, то их геометрическая сумма равна:
\(
|\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}|,
\)
при условии, что \(|\vec{m}| \geq |\vec{n}|\).
В этом случае длина результирующего вектора равна разности длин исходных векторов.

Таким образом, доказано, что:
\(
|\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}|
\)
при сонаправленных векторах, и
\(
|\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}|
\)
при противоположно направленных векторах.

Рассмотрим задачу и докажем утверждение для двух случаев:
1. Векторы \(\vec{m}\) и \(\vec{n}\) сонаправлены.
2. Векторы \(\vec{m}\) и \(\vec{n}\) противоположно направлены.

Дано:
\(\vec{m}\) и \(\vec{n}\) — векторы, \( |\vec{m}| \) — длина вектора \(\vec{m}\), \( |\vec{n}| \) — длина вектора \(\vec{n}\).

Необходимо доказать:
Если \(\vec{m}\) и \(\vec{n}\) сонаправлены, то
\(
|\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}|.
\)
Если \(\vec{m}\) и \(\vec{n}\) противоположно направлены, то при условии \( |\vec{m}| \geq |\vec{n}| \):
\(
|\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}|.
\)

Решение:

1. Рассмотрим случай, когда векторы \(\vec{m}\) и \(\vec{n}\) сонаправлены.
В этом случае угол между векторами равен \(0^\circ\), и их сумма равна вектору, длина которого равна сумме длин этих векторов.
Запишем:
\(
\vec{m} + \vec{n} = \vec{m} + \vec{n}.
\)
Так как векторы сонаправлены, их длины складываются:
\(
|\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}|.
\)
Доказано.

2. Рассмотрим случай, когда векторы \(\vec{m}\) и \(\vec{n}\) противоположно направлены.
В этом случае угол между векторами равен \(180^\circ\), и их сумма равна вектору, длина которого равна разности длин этих векторов.
Запишем:
\(
\vec{m} + \vec{n} = \vec{m} — \vec{n}.
\)
Так как векторы противоположно направлены, их длины вычитаются:
\(
|\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}|,
\)
при условии \( |\vec{m}| \geq |\vec{n}| \).
Доказано.

Ответ:
Если \(\vec{m}\) и \(\vec{n}\) сонаправлены, то
\(
|\vec{m} + \vec{n}| = |\vec{m}| + |\vec{n}|.
\)
Если \(\vec{m}\) и \(\vec{n}\) противоположно направлены, то при условии \( |\vec{m}| \geq |\vec{n}| \):
\(
|\vec{m} + \vec{n}| = |\vec{m}| — |\vec{n}|.
\)