ГДЗ по Геометрии 9 класс Номер 799 Атанасян — Подробные Ответы

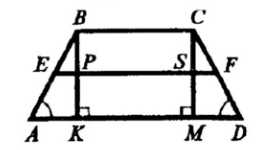
Дана равнобедренная трапеция \(ABCD\). Перпендикуляр, проведённый из вершины \(B\) к большему основанию \(AD\), делит это основание на два отрезка, больший из которых равен \(7 \, \text{см}\). Найдите среднюю линию трапеции.

Дано: \(ABCD\) — равнобедренная трапеция, \(BH\) — перпендикуляр к \(AD\), \(AB = CD\), \(HD = 7 \, \text{см}\).
Найти: \(MN\).

Решение:

По определению средней линии трапеции:
\[
MN = \frac{1}{2} (AD + BC).
\]

Средняя линия трапеции \(MN\) также состоит из средней линии треугольника \(ABH\) (\(MS\)) и средней линии треугольника \(CFD\) (\(PN\)), а также высоты прямоугольника (\(SP = HF\)).
Средняя линия треугольника \(ABH\):
\[
MS = \frac{1}{2} AH.
\]
Средняя линия треугольника \(CFD\):
\[
PN = \frac{1}{2} FD.
\]
Так как треугольники \(ABH\) и \(CFD\) равны, то \(AH = FD\).
Следовательно:
\[
MN = MS + SP + PN = FD + HF = HD = 7 \, \text{см}.
\]

Ответ: \(MN = 7 \, \text{см}\).

Дано: трапеция \(ABCD\) — равнобедренная, \(AB = CD\), \(BH\) — перпендикуляр к \(AD\), \(HD = 7 \, \text{см}\).
Найти: \(MN\), где \(MN\) — средняя линия трапеции.

Решение:

1. Средняя линия трапеции определяется как полусумма оснований трапеции:
\(
MN = \frac{1}{2} (AD + BC).
\)
Для нахождения \(MN\) необходимо определить длины оснований \(AD\) и \(BC\).

2. Рассмотрим равнобедренную трапецию. Треугольники \(ABH\) и \(CFD\) равны, так как у них равны гипотенузы (\(AB = CD\)) и один из катетов (\(BH\) — общий). Следовательно, \(AH = FD\).

3. Средняя линия треугольника \(ABH\) равна половине длины высоты \(AH\):
\(
MS = \frac{1}{2} AH.
\)
Аналогично, средняя линия треугольника \(CFD\) равна половине длины высоты \(FD\):
\(
PN = \frac{1}{2} FD.
\)

4. Из равенства треугольников \(ABH\) и \(CFD\) следует, что \(AH = FD\). Таким образом, \(MS = PN\).

5. Высота прямоугольника \(SP\) равна длине отрезка \(HF\), который совпадает с \(HD\) (по условию \(HD = 7 \, \text{см}\)).

6. Средняя линия трапеции \(MN\) состоит из сумм средней линии треугольника \(ABH\), средней линии треугольника \(CFD\) и высоты прямоугольника \(SP\):
\(
MN = MS + SP + PN.
\)
Подставляя, получаем:
\(
MN = FD + HF.
\)
Так как \(HF = HD = 7 \, \text{см}\), то:
\(
MN = HD = 7 \, \text{см}.
\)

Ответ: \(MN = 7 \, \text{см}\).