
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 795 Атанасян — Подробные Ответы
Найдите диаметр окружности, если его концы удалены от некоторой касательной на \(18 \, \text{см}\) и \(12 \, \text{см}\).
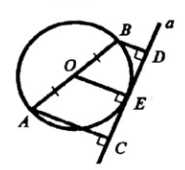
Дано: окружность \( (O; r) \), \( a \) — касательная, \( DD_1 \perp a \), \( CC_1 \perp a \), \( CC_1 = 18 \, \text{см} \), \( DD_1 = 12 \, \text{см} \). Требуется найти \( CD \).
Решение:
Трапеция \( C_1CDD_1 \) имеет параллельные стороны \( CC_1 \) и \( DD_1 \). Средняя линия трапеции \( HO \) равна полусумме оснований:
\(
HO = \frac{CC_1 + DD_1}{2} = \frac{18 + 12}{2} = 15 \, \text{см}.
\)
Радиусы \( CO \) и \( OD \) равны средней линии (\( r = HO \)):
\(
r = 15 \, \text{см}.
\)
Диаметр окружности равен удвоенному радиусу:
\(
CD = 2r = 2 \cdot 15 = 30 \, \text{см}.
\)
Ответ: \( CD = 30 \, \text{см}. \)
Дано: окружность \( (O; r) \), \( a \) — касательная, \( DD_1 \perp a \), \( CC_1 \perp a \), \( CC_1 = 18 \, \text{см} \), \( DD_1 = 12 \, \text{см} \). Требуется найти \( CD \).
Решение:
1. Рассмотрим прямые \( CC_1 \) и \( DD_1 \). Углы \( \angle C_1 \) и \( \angle D \) образуют пару односторонних углов, следовательно:
\(
\angle C_1 + \angle D = 180^\circ.
\)
Из этого следует, что \( CC_1 \parallel DD_1 \). Таким образом, фигура \( C_1CDD_1 \) является трапецией с параллельными основаниями \( CC_1 \) и \( DD_1 \).
2. По теореме Фалеса известно, что:
\(
CC_1 \parallel OH \parallel DD_1,
\)
где \( OH \) — средняя линия трапеции. Также радиусы окружности \( CO \) и \( OD \) равны, то есть:
\(
CO = OD = r.
\)
Кроме того, точки \( H \), \( C_1 \) и \( D_1 \) лежат на одной прямой, а отрезки \( C_1H \) и \( HD_1 \) равны:
\(
C_1H = HD_1.
\)
3. Найдем длину средней линии трапеции \( HO \). Средняя линия трапеции равна полусумме длин её оснований:
\(
HO = \frac{CC_1 + DD_1}{2}.
\)
Подставляем значения:
\(
HO = \frac{18 + 12}{2} = \frac{30}{2} = 15 \, \text{см}.
\)
4. Радиусы окружности равны длине средней линии трапеции:
\(
CO = OD = OH = r = 15 \, \text{см}.
\)
5. Диаметр окружности равен удвоенному радиусу:
\(
CD = 2r = 2 \cdot 15 = 30 \, \text{см}.
\)
Ответ: \( CD = 30 \, \text{см}. \)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!