ГДЗ по Геометрии 9 класс Номер 794 Атанасян — Подробные Ответы

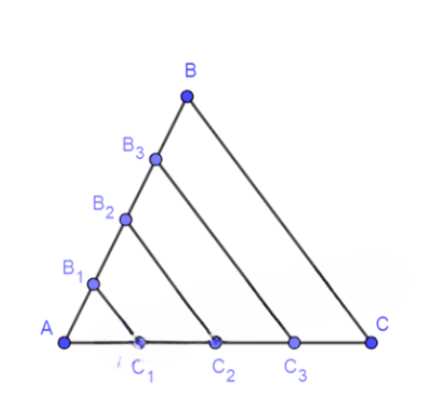
Сторона \(AB\) треугольника \(ABC\) разделена на четыре равные части и через точки деления проведены прямые, параллельные стороне \(BC\). Стороны \(AB\) и \(AC\) треугольника отсекают на этих параллельных прямых три отрезка, наименьший из которых равен \(3,4 \, \text{см}\). Найдите два других отрезка.

Дано:
\(\triangle ABC\);
\(AB_1 = B_1B_2 = B_2B_3 = B_3B\);
\(BC \parallel B_3C_3 \parallel B_2C_2 \parallel B_1C_1\);
\(B_1C_1 = 3,4 \, \text{см}\).

Решение:
1) По теореме Фалеса:
\(
AC_1 = C_1C_2 = C_2C_3 = C_3C.
\)

2) Рассматриваем \(\triangle AB_2C_2\):
\(
B_1C_1 = \frac{B_2C_2}{2}.
\)
Отсюда:
\(
B_2C_2 = 2 \cdot 3,4 = 6,8 \, \text{см}.
\)

3) Рассматриваем трапецию \(C_2B_2BC\):
\(
BC = 2 \cdot 6,8 = 13,6 \, \text{см}.
\)
Средняя линия трапеции:
\(
B_3C_3 = \frac{B_2C_2 + BC}{2} = \frac{6,8 + 13,6}{2} = 10,2 \, \text{см}.
\)

Ответ:
\(B_2C_2 = 6,8 \, \text{см}; \quad B_3C_3 = 10,2 \, \text{см}\).

Дано:
Треугольник \( \triangle ABC \), в котором \( AB_1 = B_1B_2 = B_2B_3 = B_3B \),
\( BC \parallel B_3C_3 \parallel B_2C_2 \parallel B_1C_1 \),
\( B_1C_1 = 3,4 \, \text{см} \).

Найти: \( B_2C_2 \) и \( B_3C_3 \).

Решение:
1. Согласно условию задачи, отрезки \( AB_1 = B_1B_2 = B_2B_3 = B_3B \) равны между собой. Кроме того, \( BC \parallel B_3C_3 \parallel B_2C_2 \parallel B_1C_1 \). Это означает, что данные линии параллельны, а точки \( B_1, B_2, B_3 \) делят сторону \( AB \) на равные части. Аналогично, точки \( C_1, C_2, C_3 \) делят сторону \( AC \) на равные части.

2. По теореме Фалеса, если параллельные линии пересекают две стороны угла, то отрезки, на которые они делят одну сторону, пропорциональны отрезкам, на которые они делят другую сторону. Таким образом,
\(
AC_1 = C_1C_2 = C_2C_3 = C_3C.
\)

3. Рассмотрим треугольник \( \triangle AB_2C_2 \), где \( B_1C_1 \) является средней линией. Средняя линия треугольника соединяет середины двух его сторон и параллельна третьей стороне. При этом длина средней линии равна половине длины третьей стороны. То есть:
\(
B_1C_1 = \frac{B_2C_2}{2}.
\)
Подставим значение \( B_1C_1 = 3,4 \, \text{см} \):
\(
B_2C_2 = 2 \cdot 3,4 = 6,8 \, \text{см}.
\)

4. Рассмотрим трапецию \( C_2B_2BC \), в которой \( B_3C_3 \) является средней линией. Средняя линия трапеции равна полусумме оснований трапеции. Основаниями трапеции являются \( B_2C_2 \) и \( BC \). Найдем длину \( BC \):
\(
BC = 2 \cdot B_2C_2 = 2 \cdot 6,8 = 13,6 \, \text{см}.
\)
Теперь вычислим длину средней линии \( B_3C_3 \):
\(
B_3C_3 = \frac{B_2C_2 + BC}{2} = \frac{6,8 + 13,6}{2}.
\)
Сложим основания:
\(
B_2C_2 + BC = 6,8 + 13,6 = 20,4 \, \text{см}.
\)
Разделим на два:
\(
B_3C_3 = \frac{20,4}{2} = 10,2 \, \text{см}.
\)

Ответ:
\( B_2C_2 = 6,8 \, \text{см}; \quad B_3C_3 = 10,2 \, \text{см}. \)