ГДЗ по Геометрии 9 класс Номер 792 Атанасян — Подробные Ответы

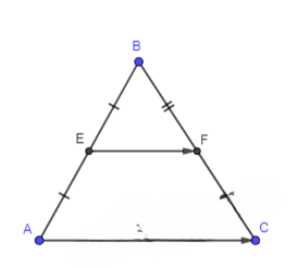
Докажите теорему о средней линии треугольника (п. 64).

Дано:
\(\triangle ABC\);
\(AE = EB\);
\(BF = FC\).

Доказательство:
По правилу треугольников:
\(
AC = AB + BC.
\)
Так как \(EF = EB + BF\), то:
\(
EF = \frac{1}{2}AB + \frac{1}{2}BC = \frac{1}{2}(AB + BC) = \frac{1}{2}AC.
\)
Следовательно, \(EF \parallel AC\), так как коллинеарные, и \(|EF| = \frac{1}{2}|AC|\).

Что и требовалось доказать.

Дано:
\(\triangle ABC\);
\(AE = EB\);
\(BF = FC\).

Доказательство:

1. Рассмотрим треугольник \(\triangle ABC\). Согласно правилу треугольников, длина стороны \(AC\) может быть выражена через сумму двух отрезков:
\(
AC = AB + BC.
\)

2. Так как точки \(E\) и \(F\) делят стороны \(AB\) и \(BC\) пополам, то:
\(
AE = EB = \frac{1}{2}AB, \quad BF = FC = \frac{1}{2}BC.
\)

3. Рассмотрим отрезок \(EF\), который состоит из суммы двух отрезков:
\(
EF = EB + BF.
\)
Подставим значения \(EB\) и \(BF\):
\(
EF = \frac{1}{2}AB + \frac{1}{2}BC.
\)

4. Вынесем общий множитель \(\frac{1}{2}\):
\(
EF = \frac{1}{2}(AB + BC).
\)

5. Согласно пункту 1, \(AB + BC = AC\). Тогда:
\(
EF = \frac{1}{2}AC.
\)

6. Следовательно, длина отрезка \(EF\) равна половине длины отрезка \(AC\):
\(
|EF| = \frac{1}{2}|AC|.
\)

7. Кроме того, так как \(EF\) и \(AC\) лежат на одной прямой, то они коллинеарны:
\(
EF \parallel AC.
\)

Ответ: \(EF \parallel AC\) и \(|EF| = \frac{1}{2}|AC|\).
Что и требовалось доказать.