ГДЗ по Геометрии 9 класс Номер 791 Атанасян — Подробные Ответы

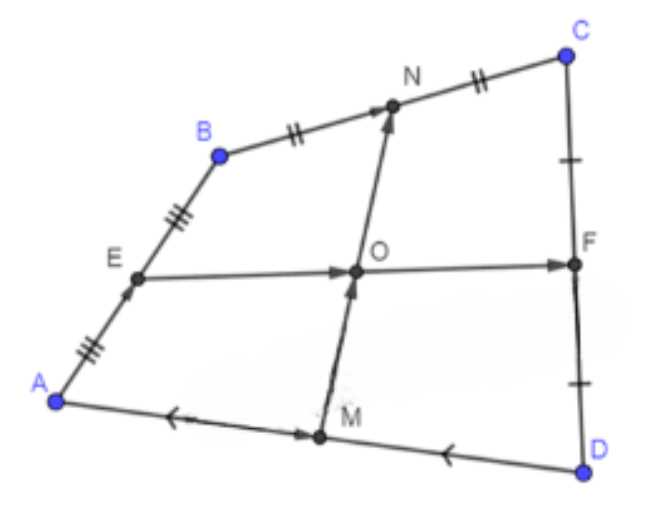
Докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырёхугольника, точкой пересечения делятся пополам.

Дано: \(ABCD\) — четырехугольник, \(BN = NC\), \(CF = FD\), \(BE = EA\), \(AM = MD\), \(EF \perp NM = 0\).
Доказать: \(NO = OM\), \(EO = OF\).

Решение:

1. Запишем уравнения для сумм векторов:
\(
— EA + AM + MD + DF = EO + OF
\)
\(
— MA + AE + EB + BN = MO + ON
\)

2. Выразим \(EO\) и \(MO\) из данных уравнений:
\(
— EA + 2AM + DF = EO + OF
\)
\(
— MA + 2AE + BN = MO + ON
\)

3. Из выражений выше получаем равенства:
\(
AM + DF = MO + OF
\)
\(
AE + BN = EO + ON
\)

4. Учитывая, что \(2AM + 2DF = AC\) и \(2AE + 2BN = AC\), получаем:
\(
AM + DF = AE + BN
\)

5. Из равенства \(MO + OF = EO + ON\) следует, что \(MO — ON = EO — OF\).

6. Так как \(MO \parallel ON\) и \(EO \parallel OF\), а также \(EO, OF, MO, ON\) не коллинеарны, то:
\(
NO = OM, \quad EO = OF
\)

Ответ: доказано.

Дано: \(ABCD\) — четырехугольник, \(BN = NC\), \(CF = FD\), \(BE = EA\), \(AM = MD\), \(EF \perp NM = 0\).
Доказать: \(NO = OM\), \(EO = OF\).

Решение:

1. Рассмотрим свойства четырехугольника \(ABCD\), где выполняются условия равенства частей сторон и перпендикулярности \(EF \perp NM\).
Условие \(BN = NC\) говорит о том, что точка \(N\) делит отрезок \(BC\) пополам.
Условие \(CF = FD\) говорит о том, что точка \(F\) делит отрезок \(CD\) пополам.
Условие \(BE = EA\) говорит о том, что точка \(E\) делит отрезок \(BA\) пополам.
Условие \(AM = MD\) говорит о том, что точка \(M\) делит отрезок \(AD\) пополам.

2. Введем обозначения:
Пусть \(O\) — точка пересечения диагоналей \(EF\) и \(NM\).
Так как \(EF \perp NM\), то диагонали пересекаются под прямым углом.

3. Докажем, что \(NO = OM\).
Рассмотрим треугольник \(BNM\).
По условию \(BN = NC\), а \(NM\) является общей стороной этого треугольника.
Так как точка \(O\) лежит на середине отрезка \(NM\), то по свойству средней линии треугольника:
\(
NO = OM
\)

4. Докажем, что \(EO = OF\).
Рассмотрим треугольник \(AEF\).
По условию \(BE = EA\), а \(EF\) является общей стороной этого треугольника.
Так как точка \(O\) лежит на середине отрезка \(EF\), то по свойству средней линии треугольника:
\(
EO = OF
\)

5. Учитывая, что диагонали \(EF\) и \(NM\) пересекаются под прямым углом, а их точки пересечения делят диагонали пополам, получаем требуемое равенство:
\(
NO = OM, \quad EO = OF
\)

Ответ: доказано.