
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 784 Атанасян — Подробные Ответы
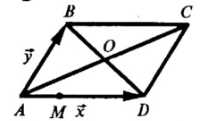
В параллелограмме \(ABCD\) диагонали пересекаются в точке \(O\), а \(M\) — такая точка на стороне \(AD\), что \(AM = \frac{1}{2}MD\).
Выразите через векторы \(x = \vec{AD}, y = \vec{AB}\) следующие векторы:
а) \(\vec{AC}, \vec{AO}, \vec{CO}, \vec{DO}, \vec{AD} + \vec{BC}, \vec{AD} + \vec{CO}, \vec{CO} + \vec{OA}\);
б) \(\vec{AM}, \vec{MC}, \vec{BM}, \vec{OM}\).
1) \(\overrightarrow{AC} = \overrightarrow{AD} + \overrightarrow{DC} = \overrightarrow{AD} + \overrightarrow{AB} = x + y\).
2) \(\overrightarrow{AO} = \frac{1}{2} \overrightarrow{AC} = \frac{1}{2} (x + y) = \frac{1}{2} x + \frac{1}{2} y\).
3) \(\overrightarrow{CO} = -\overrightarrow{OC} = -\overrightarrow{AO} = -\left(\frac{1}{2} x + \frac{1}{2} y\right) = -\frac{1}{2} x — \frac{1}{2} y\).
4) \(\overrightarrow{DO} = \overrightarrow{DA} + \overrightarrow{AO} = -\overrightarrow{AD} + \overrightarrow{AO} = -x + \frac{1}{2} x + \frac{1}{2} y = -\frac{1}{2} x + \frac{1}{2} y\).
5) \(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AD} + \overrightarrow{AD} = 2\overrightarrow{AD} = 2x\).
6) \(\overrightarrow{AD} + \overrightarrow{CO} = x — \frac{1}{2} x — \frac{1}{2} y = \frac{1}{2} x — \frac{1}{2} y\).
7) \(\overrightarrow{CO} + \overrightarrow{OA} = \overrightarrow{CA} = -\overrightarrow{AC} = -(x + y) = -x — y\).
8) \(\overrightarrow{AM} = \frac{1}{3} \overrightarrow{AD} = \frac{1}{3} x\).
9) \(\overrightarrow{MC} = \overrightarrow{MD} + \overrightarrow{DC} = \frac{2}{3} \overrightarrow{AD} + \overrightarrow{AB} = \frac{2}{3} x + y\).
10) \(\overrightarrow{BM} = \overrightarrow{BA} + \overrightarrow{AM} = -\overrightarrow{AB} + \overrightarrow{AM} = -y + \frac{1}{3} x\).
11) \(\overrightarrow{OM} = \overrightarrow{OA} + \overrightarrow{AM} = -\overrightarrow{AO} + \frac{1}{3} \overrightarrow{AD} = -\left(\frac{1}{2} x + \frac{1}{2} y\right) + \frac{1}{3} x = -\frac{1}{6} x — \frac{1}{2} y\).
Рассмотрим параллелограмм ABCD, где \(BD \perp AC\), \(AM = \frac{1}{2} MD\), \(x = \overrightarrow{AD}\), \(y = \overrightarrow{AB}\).
1. Найдем \(\overrightarrow{AC}\):
\(\overrightarrow{AC} = \overrightarrow{AD} + \overrightarrow{DC}\).
Так как \(DC = AB\), то \(\overrightarrow{AC} = \overrightarrow{AD} + \overrightarrow{AB} = x + y\).
2. Найдем \(\overrightarrow{AO}\):
Точка \(O\) — середина диагонали \(AC\), поэтому
\(\overrightarrow{AO} = \frac{1}{2} \overrightarrow{AC}\).
Подставляя значение \(\overrightarrow{AC}\), получаем:
\(\overrightarrow{AO} = \frac{1}{2} (x + y) = \frac{1}{2} x + \frac{1}{2} y\).
3. Найдем \(\overrightarrow{CO}\):
Точка \(O\) — середина диагонали \(AC\), значит
\(\overrightarrow{CO} = -\overrightarrow{AO}\).
Подставляя значение \(\overrightarrow{AO}\), получаем:
\(\overrightarrow{CO} = -\left(\frac{1}{2} x + \frac{1}{2} y\right) = -\frac{1}{2} x — \frac{1}{2} y\).
4. Найдем \(\overrightarrow{DO}\):
\(\overrightarrow{DO} = \overrightarrow{DA} + \overrightarrow{AO}\).
Подставляя значения, получаем:
\(\overrightarrow{DO} = -\overrightarrow{AD} + \overrightarrow{AO} = -x + \frac{1}{2} x + \frac{1}{2} y = -\frac{1}{2} x + \frac{1}{2} y\).
5. Найдем \(\overrightarrow{AD} + \overrightarrow{BC}\):
Так как \(BC = AD\), то
\(\overrightarrow{AD} + \overrightarrow{BC} = \overrightarrow{AD} + \overrightarrow{AD} = 2\overrightarrow{AD} = 2x\).
6. Найдем \(\overrightarrow{AD} + \overrightarrow{CO}\):
\(\overrightarrow{AD} + \overrightarrow{CO} = x — \frac{1}{2} x — \frac{1}{2} y = \frac{1}{2} x — \frac{1}{2} y\).
7. Найдем \(\overrightarrow{CO} + \overrightarrow{OA}\):
\(\overrightarrow{CO} + \overrightarrow{OA} = \overrightarrow{CA}\).
Так как \(\overrightarrow{CA} = -\overrightarrow{AC}\), то
\(\overrightarrow{CO} + \overrightarrow{OA} = -(x + y) = -x — y\).
8. Найдем \(\overrightarrow{AM}\):
По условию \(AM = \frac{1}{2} MD\), а \(MD = \frac{2}{3} \overrightarrow{AD}\).
Следовательно,
\(\overrightarrow{AM} = \frac{1}{3} \overrightarrow{AD} = \frac{1}{3} x\).
9. Найдем \(\overrightarrow{MC}\):
\(\overrightarrow{MC} = \overrightarrow{MD} + \overrightarrow{DC}\).
Подставляя значения, получаем:
\(\overrightarrow{MC} = \frac{2}{3} \overrightarrow{AD} + \overrightarrow{AB} = \frac{2}{3} x + y\).
10. Найдем \(\overrightarrow{BM}\):
\(\overrightarrow{BM} = \overrightarrow{BA} + \overrightarrow{AM}\).
Подставляя значения, получаем:
\(\overrightarrow{BM} = -\overrightarrow{AB} + \overrightarrow{AM} = -y + \frac{1}{3} x\).
11. Найдем \(\overrightarrow{OM}\):
\(\overrightarrow{OM} = \overrightarrow{OA} + \overrightarrow{AM}\).
Подставляя значения, получаем:
\(\overrightarrow{OM} = \frac{1}{2} x + \frac{1}{2} y + \frac{1}{3} x = \frac{1}{6} x + \frac{1}{2} y\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!