
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 778 Атанасян — Подробные Ответы
Начертите попарно неколлинеарные векторы \(\overrightarrow{a}\), \(\overrightarrow{b}\) и \(\overrightarrow{c}\). Постройте векторы:
а) \(2\overrightarrow{a} + 3\overrightarrow{b} — 4\overrightarrow{c}\);
б) \(\frac{1}{2}\overrightarrow{a} — \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\).
Для выполнения задачи необходимо построить заданные векторы с учетом их длины и направления. Рассмотрим оба случая.
а) \(2\overrightarrow{a} + 3\overrightarrow{b} — 4\overrightarrow{c}\):
1. Удлиняем вектор \(\overrightarrow{a}\) в 2 раза, получая \(2\overrightarrow{a}\).
2. Удлиняем вектор \(\overrightarrow{b}\) в 3 раза, получая \(3\overrightarrow{b}\).
3. Удлиняем вектор \(\overrightarrow{c}\) в 4 раза и направляем его в противоположную сторону, получая \(-4\overrightarrow{c}\).
4. Складываем \(2\overrightarrow{a}\), \(3\overrightarrow{b}\) и \(-4\overrightarrow{c}\) по правилу сложения векторов (переносим начало каждого следующего вектора к концу предыдущего).
Итоговый вектор направлен от начала \(2\overrightarrow{a}\) к конечной точке суммы.
б) \(\frac{1}{2}\overrightarrow{a} — \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\):
1. Удлиняем вектор \(\overrightarrow{a}\) до половины его длины, получая \(\frac{1}{2}\overrightarrow{a}\).
2. Направляем вектор \(\overrightarrow{b}\) в противоположную сторону, получая \(-\overrightarrow{b}\).
3. Удлиняем вектор \(\overrightarrow{c}\) до трети его длины, получая \(\frac{1}{3}\overrightarrow{c}\).
4. Складываем \(\frac{1}{2}\overrightarrow{a}\), \(-\overrightarrow{b}\) и \(\frac{1}{3}\overrightarrow{c}\) по правилу сложения векторов.
Итоговый вектор направлен от начала \(\frac{1}{2}\overrightarrow{a}\) к конечной точке суммы.
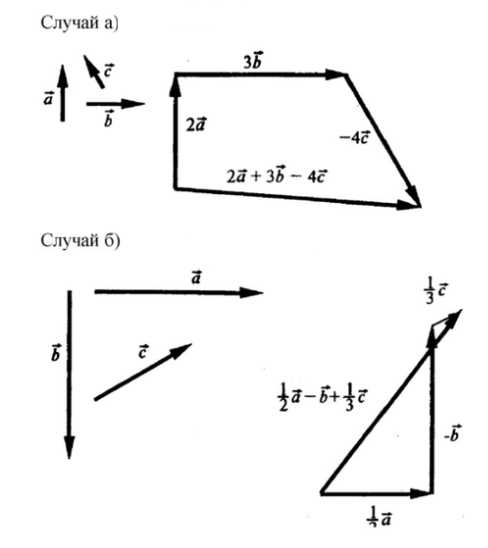
На предоставленном изображении показано графическое построение обоих случаев.
Для решения задачи разберем оба случая подробно, с учетом всех этапов построения векторов.
а) Построение вектора \(2\overrightarrow{a} + 3\overrightarrow{b} — 4\overrightarrow{c}\):
1. Удлиняем вектор \(\overrightarrow{a}\) в 2 раза. Это означает, что новый вектор сохраняет направление исходного вектора \(\overrightarrow{a}\), но его длина увеличивается в 2 раза. Обозначим полученный вектор как \(2\overrightarrow{a}\).
2. Удлиняем вектор \(\overrightarrow{b}\) в 3 раза. Новый вектор сохраняет направление исходного \(\overrightarrow{b}\), но его длина увеличивается в 3 раза. Обозначим полученный вектор как \(3\overrightarrow{b}\).
3. Удлиняем вектор \(\overrightarrow{c}\) в 4 раза и меняем его направление на противоположное, чтобы получить \(-4\overrightarrow{c}\). Новый вектор будет направлен в сторону, противоположную исходному \(\overrightarrow{c}\), а его длина увеличится в 4 раза.
4. Складываем \(2\overrightarrow{a}\), \(3\overrightarrow{b}\) и \(-4\overrightarrow{c}\). Для этого размещаем начало вектора \(3\overrightarrow{b}\) в конце вектора \(2\overrightarrow{a}\), а затем начало вектора \(-4\overrightarrow{c}\) в конце вектора \(3\overrightarrow{b}\).
5. Итоговый вектор, который соединяет начало \(2\overrightarrow{a}\) с конечной точкой суммы, будет результатом операции \(2\overrightarrow{a} + 3\overrightarrow{b} — 4\overrightarrow{c}\).
б) Построение вектора \(\frac{1}{2}\overrightarrow{a} — \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\):
1. Удлиняем вектор \(\overrightarrow{a}\) до половины его длины. Новый вектор сохраняет направление исходного \(\overrightarrow{a}\), но его длина уменьшается в 2 раза. Обозначим полученный вектор как \(\frac{1}{2}\overrightarrow{a}\).
2. Меняем направление вектора \(\overrightarrow{b}\) на противоположное, чтобы получить \(-\overrightarrow{b}\). Новый вектор будет направлен в сторону, противоположную исходному \(\overrightarrow{b}\), а его длина остается неизменной.
3. Удлиняем вектор \(\overrightarrow{c}\) до трети его длины. Новый вектор сохраняет направление исходного \(\overrightarrow{c}\), но его длина уменьшается в 3 раза. Обозначим полученный вектор как \(\frac{1}{3}\overrightarrow{c}\).
4. Складываем \(\frac{1}{2}\overrightarrow{a}\), \(-\overrightarrow{b}\) и \(\frac{1}{3}\overrightarrow{c}\). Для этого размещаем начало вектора \(-\overrightarrow{b}\) в конце вектора \(\frac{1}{2}\overrightarrow{a}\), а затем начало вектора \(\frac{1}{3}\overrightarrow{c}\) в конце вектора \(-\overrightarrow{b}\).
5. Итоговый вектор, который соединяет начало \(\frac{1}{2}\overrightarrow{a}\) с конечной точкой суммы, будет результатом операции \(\frac{1}{2}\overrightarrow{a} — \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\).
На изображении показано графическое построение обоих случаев. В первом случае итоговый вектор обозначен как \(2\overrightarrow{a} + 3\overrightarrow{b} — 4\overrightarrow{c}\), а во втором — как \(\frac{1}{2}\overrightarrow{a} — \overrightarrow{b} + \frac{1}{3}\overrightarrow{c}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!