ГДЗ по Геометрии 9 класс Номер 776 Атанасян — Подробные Ответы

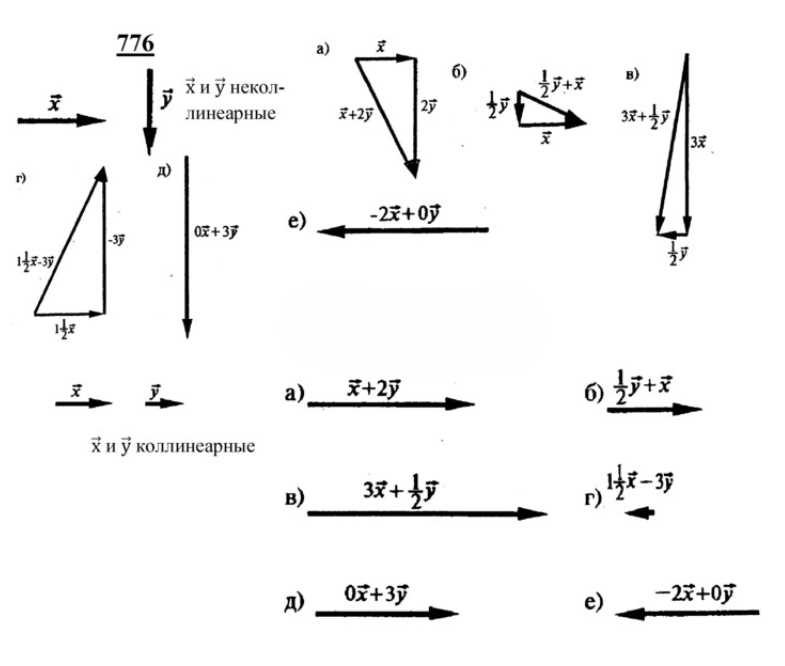
776 Начертите два неколлинеарных вектора \(\overrightarrow{x}\) и \(\overrightarrow{y}\) и постройте векторы:
а) \(\overrightarrow{x} + 2\overrightarrow{y}\);
б) \(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x}\);
в) \(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y}\);
г) \(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y}\);
д) \(0\overrightarrow{x} + 4\overrightarrow{y}\);
е) \(-2\overrightarrow{x} + 0\overrightarrow{y}\).

Выполните задания а) – е) для двух коллинеарных ненулевых векторов \(\overrightarrow{x}\) и \(\overrightarrow{y}\).

Для выполнения задания:

а) \(\overrightarrow{x} + 2\overrightarrow{y}\):
Сложение двух векторов выполняется так, что к концу вектора \(\overrightarrow{x}\) добавляется удвоенный вектор \(\overrightarrow{y}\). Итоговый вектор направлен от начала \(\overrightarrow{x}\) к конечной точке суммы.

б) \(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x}\):
Вектор \(\frac{1}{2}\overrightarrow{y}\) имеет половину длины \(\overrightarrow{y}\). Складываем его с вектором \(\overrightarrow{x}\), получая результат.

в) \(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y}\):
Удлиняем вектор \(\overrightarrow{x}\) в три раза и добавляем к нему половину длины \(\overrightarrow{y}\).

г) \(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y}\):
Вектор \(\frac{1}{2}\overrightarrow{x}\) имеет половину длины \(\overrightarrow{x}\). Вычитаем из него утроенный вектор \(\overrightarrow{y}\), направленный в противоположную сторону.

д) \(0\overrightarrow{x} + 4\overrightarrow{y}\):
Вектор \(0\overrightarrow{x}\) равен нулю, результатом является \(4\overrightarrow{y}\), направленный вверх.

е) \(-2\overrightarrow{x} + 0\overrightarrow{y}\):
Вектор \(0\overrightarrow{y}\) равен нулю, а \(-2\overrightarrow{x}\) — это удвоенный вектор \(\overrightarrow{x}\), но направленный в противоположную сторону.

Для коллинеарных векторов:
а) \(\overrightarrow{x} + 2\overrightarrow{y} = \overrightarrow{x} + 2k\overrightarrow{x} = (1 + 2k)\overrightarrow{x}\), где \(k\) — коэффициент пропорциональности.
б) \(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x} = \frac{k}{2}\overrightarrow{x} + \overrightarrow{x} = (1 + \frac{k}{2})\overrightarrow{x}\).
в) \(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y} = 3\overrightarrow{x} + \frac{k}{2}\overrightarrow{x} = (3 + \frac{k}{2})\overrightarrow{x}\).
г) \(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y} = \frac{1}{2}\overrightarrow{x} — 3k\overrightarrow{x} = (\frac{1}{2} — 3k)\overrightarrow{x}\).
д) \(0\overrightarrow{x} + 4\overrightarrow{y} = 0 + 4k\overrightarrow{x} = 4k\overrightarrow{x}\).
е) \(-2\overrightarrow{x} + 0\overrightarrow{y} = -2\overrightarrow{x} + 0 = -2\overrightarrow{x}\).

Для выполнения задачи необходимо подробно рассмотреть каждый случай. Начнем с двух неколлинеарных векторов \(\overrightarrow{x}\) и \(\overrightarrow{y}\), которые лежат на плоскости. Пусть \(\overrightarrow{x}\) направлен вправо, а \(\overrightarrow{y}\) направлен вверх. Все операции с векторами выполняются графически или аналитически.

а) \(\overrightarrow{x} + 2\overrightarrow{y}\)
Сложение векторов выполняется следующим образом:
1. Вектор \(\overrightarrow{x}\) остается без изменений.
2. Вектор \(2\overrightarrow{y}\) строится путем удлинения вектора \(\overrightarrow{y}\) в два раза.
3. К концу \(\overrightarrow{x}\) прибавляется \(2\overrightarrow{y}\).
Итоговый вектор направлен от начала \(\overrightarrow{x}\) к конечной точке суммы.

б) \(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x}\)
1. Вектор \(\frac{1}{2}\overrightarrow{y}\) строится как половина длины \(\overrightarrow{y}\).
2. Этот вектор прибавляется к \(\overrightarrow{x}\), то есть его начало размещается в конце \(\overrightarrow{x}\).
Итоговый вектор направлен от начала \(\overrightarrow{x}\) к конечной точке суммы.

в) \(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y}\)
1. Вектор \(3\overrightarrow{x}\) строится путем удлинения \(\overrightarrow{x}\) в три раза.
2. Вектор \(\frac{1}{2}\overrightarrow{y}\) строится как половина длины \(\overrightarrow{y}\).
3. Складываем \(3\overrightarrow{x}\) и \(\frac{1}{2}\overrightarrow{y}\), размещая начало второго вектора в конце первого.
Итоговый вектор направлен от начала \(3\overrightarrow{x}\) к конечной точке суммы.

г) \(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y}\)
1. Вектор \(\frac{1}{2}\overrightarrow{x}\) строится как половина длины \(\overrightarrow{x}\).
2. Вектор \(3\overrightarrow{y}\) строится путем удлинения \(\overrightarrow{y}\) в три раза, но затем он направляется в противоположную сторону (вычитание).
3. Складываем \(\frac{1}{2}\overrightarrow{x}\) и \(-3\overrightarrow{y}\), размещая начало второго вектора в конце первого.
Итоговый вектор направлен от начала \(\frac{1}{2}\overrightarrow{x}\) к конечной точке суммы.

д) \(0\overrightarrow{x} + 4\overrightarrow{y}\)
1. Вектор \(0\overrightarrow{x}\) равен нулю, то есть его длина равна нулю, и он не изменяет результат.
2. Вектор \(4\overrightarrow{y}\) строится путем удлинения \(\overrightarrow{y}\) в четыре раза.
Итоговый вектор совпадает с \(4\overrightarrow{y}\).

е) \(-2\overrightarrow{x} + 0\overrightarrow{y}\)
1. Вектор \(0\overrightarrow{y}\) равен нулю, то есть его длина равна нулю, и он не изменяет результат.
2. Вектор \(-2\overrightarrow{x}\) строится путем удлинения \(\overrightarrow{x}\) в два раза и направления в противоположную сторону.
Итоговый вектор совпадает с \(-2\overrightarrow{x}\).

Теперь рассмотрим случай для двух коллинеарных векторов \(\overrightarrow{x}\) и \(\overrightarrow{y}\). Пусть \(\overrightarrow{y} = k\overrightarrow{x}\), где \(k\) — коэффициент пропорциональности.

а) \(\overrightarrow{x} + 2\overrightarrow{y}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(\overrightarrow{x} + 2\overrightarrow{y} = \overrightarrow{x} + 2k\overrightarrow{x} = (1 + 2k)\overrightarrow{x}\).

б) \(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(\frac{1}{2}\overrightarrow{y} + \overrightarrow{x} = \frac{k}{2}\overrightarrow{x} + \overrightarrow{x} = (1 + \frac{k}{2})\overrightarrow{x}\).
Если \(k\) дробное, результат можно представить в виде смешанного числа.

в) \(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(3\overrightarrow{x} + \frac{1}{2}\overrightarrow{y} = 3\overrightarrow{x} + \frac{k}{2}\overrightarrow{x} = (3 + \frac{k}{2})\overrightarrow{x}\).
Если \(k\) дробное, результат можно представить в виде смешанного числа.

г) \(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(\frac{1}{2}\overrightarrow{x} — 3\overrightarrow{y} = \frac{1}{2}\overrightarrow{x} — 3k\overrightarrow{x} = (\frac{1}{2} — 3k)\overrightarrow{x}\).
Если \(k\) дробное, результат можно представить в виде смешанного числа.

д) \(0\overrightarrow{x} + 4\overrightarrow{y}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(0\overrightarrow{x} + 4\overrightarrow{y} = 0 + 4k\overrightarrow{x} = 4k\overrightarrow{x}\).
Если \(k\) дробное, результат можно представить в виде смешанного числа.

е) \(-2\overrightarrow{x} + 0\overrightarrow{y}\)
Подставляем \(\overrightarrow{y} = k\overrightarrow{x}\):
\(-2\overrightarrow{x} + 0\overrightarrow{y} = -2\overrightarrow{x} + 0 = -2\overrightarrow{x}\).