
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 774 Атанасян — Подробные Ответы
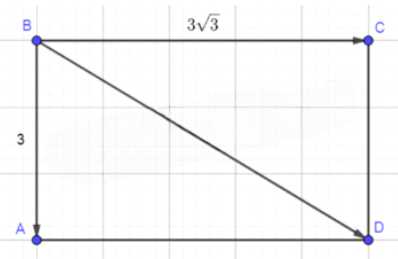
Парашютист спускался на землю со скоростью 3 м/с. Порывом ветра его начинает относить в сторону со скоростью \(3\sqrt{3}\) м/с. Под каким углом к вертикали спускается парашютист?
Дано:
\(\overrightarrow{BA} = 3 \, \text{м/с}, \overrightarrow{BC} = 3\sqrt{3} \, \text{м/с}\).
Найти: \(\angle ABD\).
Решение:
1. \(ABCD\) — прямоугольник, следовательно:
\(
BC = AD = 3\sqrt{3} \, \text{м/с}.
\)
2. По теореме Пифагора:
\(
BD = \sqrt{AB^2 + AD^2} = \sqrt{3^2 + (3\sqrt{3})^2} = \sqrt{9 + 27} = \sqrt{36} = 6 \, \text{м/с}.
\)
3. \(\frac{AB}{BD} = \frac{3}{6} = \frac{1}{2}\), значит \(\angle BDA = 30^\circ\) (по свойству прямоугольного треугольника).
4. \(\angle ABD = 90^\circ — \angle BDA = 90^\circ — 30^\circ = 60^\circ\).
Ответ: Парашютист спускается под углом \(30^\circ\).
Дано:
\(\overrightarrow{BA} = 3 \, \text{м/с}\), \(\overrightarrow{BC} = 3\sqrt{3} \, \text{м/с}\).
Найти: \(\angle ABD\).
Решение:
1. Рассмотрим фигуру \(ABCD\). Так как \(AB \perp BC\), то \(ABCD\) является прямоугольником. Следовательно, противоположные стороны равны, то есть
\(
BC = AD = 3\sqrt{3} \, \text{м/с}.
\)
2. Найдем длину диагонали \(BD\) по теореме Пифагора:
\(
BD = \sqrt{AB^2 + AD^2}.
\)
Подставляем значения:
\(
BD = \sqrt{3^2 + (3\sqrt{3})^2}.
\)
Выполним вычисления:
\(
BD = \sqrt{9 + 27} = \sqrt{36} = 6 \, \text{м/с}.
\)
3. Рассмотрим треугольник \(ABD\). Он является прямоугольным, так как угол \(BAD = 90^\circ\). Для нахождения угла \(\angle BDA\) воспользуемся определением синуса:
\(
\sin(\angle BDA) = \frac{AB}{BD}.
\)
Подставляем значения:
\(
\sin(\angle BDA) = \frac{3}{6} = \frac{1}{2}.
\)
Из таблицы значений тригонометрических функций находим, что
\(
\angle BDA = 30^\circ.
\)
4. Теперь найдем угол \(\angle ABD\):
\(
\angle ABD = 90^\circ — \angle BDA.
\)
Подставляем значение:
\(
\angle ABD = 90^\circ — 30^\circ = 60^\circ.
\)
Ответ: Парашютист спускается под углом \(30^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!