
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 771 Атанасян — Подробные Ответы
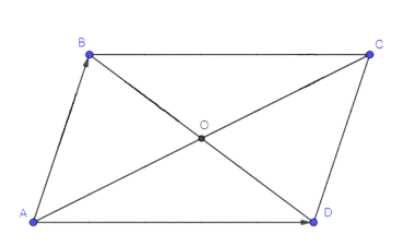
Выразите через векторы \(\vec{a} = \overrightarrow{AB}\) и \(\vec{b} = \overrightarrow{AD}\) векторы: \(\overrightarrow{DC} + \overrightarrow{CB}, \ \overrightarrow{BO} + \overrightarrow{OC}, \ \overrightarrow{BO} — \overrightarrow{OC}, \ \overrightarrow{BA} — \overrightarrow{DA}\).
Дано: \(ABCD\) — параллелограмм.
\(\vec{a} = \overrightarrow{AB}, \ \vec{b} = \overrightarrow{AD}\).
Необходимо выразить: \(DC + CB\), \(BO + OC\), \(BO — OC\), \(BA — DA\).
Решение:
1) \(DC + CB = \overrightarrow{DB} = \overrightarrow{AB} — \overrightarrow{AD} = \vec{a} — \vec{b}\).
2) \(BO + OC = \overrightarrow{BC} = \overrightarrow{AD} = \vec{b}\).
3) \(BO — OC = \overrightarrow{BO} — \overrightarrow{OC} = \overrightarrow{BO} — (-\overrightarrow{DA}) = \)
\(=\overrightarrow{BO} + \overrightarrow{OA} = \overrightarrow{BA} = -\overrightarrow{AB} = -\vec{a}\).
4) \(BA — DA = \overrightarrow{BA} — \overrightarrow{DA} = \overrightarrow{BA} — (-\overrightarrow{AD}) =\)
\(= \overrightarrow{BA} + \overrightarrow{AD} = -\overrightarrow{AB} + \overrightarrow{AD} = -\vec{a} + \vec{b} = \vec{b} — \vec{a}\).
Ответ:
\(DC + CB = \vec{a} — \vec{b}\);
\(BO + OC = \vec{b}\);
\(BO — OC = -\vec{a}\);
\(BA — DA = \vec{b} — \vec{a}\).
Дано: \(ABCD\) — параллелограмм, \(\vec{a} = \overrightarrow{AB}, \ \vec{b} = \overrightarrow{AD}\). Требуется выразить: \(DC + CB\), \(BO + OC\), \(BO — OC\), \(BA — DA\).
Решение:
1. Выражение \(DC + CB\):
Согласно правилу треугольника, сумма векторов \(DC + CB\) равна вектору \(\overrightarrow{DB}\), так как эти два вектора последовательно соединяют точки \(D\), \(C\) и \(B\).
По свойствам параллелограмма, вектор \(\overrightarrow{DB}\) можно записать как разность векторов \(\overrightarrow{AB}\) и \(\overrightarrow{AD}\):
\(
DC + CB = \overrightarrow{DB} = \overrightarrow{AB} — \overrightarrow{AD}.
\)
Подставляем обозначения:
\(
DC + CB = \vec{a} — \vec{b}.
\)
2. Выражение \(BO + OC\):
Векторы \(BO\) и \(OC\) соединяют точки \(B\), \(O\) и \(C\). По правилу треугольника их сумма равна вектору \(\overrightarrow{BC}\):
\(
BO + OC = \overrightarrow{BC}.
\)
В параллелограмме противоположные стороны равны, поэтому \(\overrightarrow{BC} = \overrightarrow{AD}\):
\(
BO + OC = \vec{b}.
\)
3. Выражение \(BO — OC\):
Разность векторов \(BO — OC\) равна вектору \(\overrightarrow{BO} — \overrightarrow{OC}\).
Вектор \(\overrightarrow{OC}\) направлен противоположно вектору \(\overrightarrow{DA}\), то есть \(\overrightarrow{OC} = -\overrightarrow{DA}\).
Подставляем это в выражение:
\(
BO — OC = \overrightarrow{BO} — (-\overrightarrow{DA}) = \overrightarrow{BO} + \overrightarrow{OA}.
\)
Сумма векторов \(\overrightarrow{BO} + \overrightarrow{OA}\) равна вектору \(\overrightarrow{BA}\):
\(
BO — OC = \overrightarrow{BA}.
\)
Вектор \(\overrightarrow{BA}\) направлен противоположно вектору \(\overrightarrow{AB}\), то есть \(\overrightarrow{BA} = -\overrightarrow{AB}\):
\(
BO — OC = -\vec{a}.
\)
4. Выражение \(BA — DA\):
Разность векторов \(BA — DA\) равна вектору \(\overrightarrow{BA} — \overrightarrow{DA}\).
Вектор \(\overrightarrow{DA}\) направлен противоположно вектору \(\overrightarrow{AD}\), то есть \(\overrightarrow{DA} = -\overrightarrow{AD}\).
Подставляем это в выражение:
\(
BA — DA = \overrightarrow{BA} — (-\overrightarrow{AD}) = \overrightarrow{BA} + \overrightarrow{AD}.
\)
Вектор \(\overrightarrow{BA}\) направлен противоположно вектору \(\overrightarrow{AB}\), то есть \(\overrightarrow{BA} = -\overrightarrow{AB}\):
\(
BA — DA = -\overrightarrow{AB} + \overrightarrow{AD}.
\)
Подставляем обозначения:
\(
BA — DA = -\vec{a} + \vec{b}.
\)
Упрощаем выражение:
\(
BA — DA = \vec{b} — \vec{a}.
\)
Ответ:
\(DC + CB = \vec{a} — \vec{b}\);
\(BO + OC = \vec{b}\);
\(BO — OC = -\vec{a}\);
\(BA — DA = \vec{b} — \vec{a}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!