ГДЗ по Геометрии 9 класс Номер 766 Атанасян — Подробные Ответы

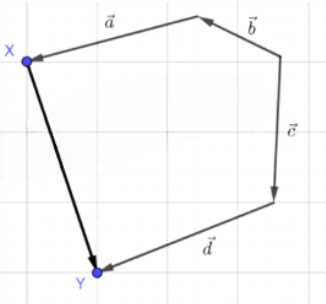
На рисунке 259 изображены векторы \( \vec{a} \), \( \vec{b} \), \( \vec{c} \), \( \vec{d} \), \( \vec{XY} \). Представьте вектор \( \vec{XY} \) в виде суммы остальных или им противоположных векторов.

Решение:

Для представления вектора \(\vec{XY}\) в виде суммы других векторов необходимо, чтобы конец каждого вектора совпадал с началом следующего.

\(
\vec{XY} = -\vec{a} — \vec{b} + \vec{c} + \vec{d}
\)

По условию задачи требуется представить вектор \(\vec{XY}\) в виде суммы:

\(
\vec{XY} = -\vec{a} + (-\vec{b}) + \vec{c} + \vec{d}
\)

Ответ:

\(
\vec{XY} = -\vec{a} + (-\vec{b}) + \vec{c} + \vec{d}
\)

Решение:

Для представления вектора \(\vec{XY}\) в виде суммы других векторов необходимо учитывать следующее:

1. Вектор \(\vec{XY}\) можно выразить через сумму других векторов, если конец каждого вектора совпадает с началом следующего. Это условие обеспечивает корректность разложения.

2. Используем правило сложения векторов: если вектора соединены «по цепочке», то их сумма равна результирующему вектору, соединяющему начало первого вектора с концом последнего.

Запишем разложение вектора \(\vec{XY}\):

\(
\vec{XY} = -\vec{a} — \vec{b} + \vec{c} + \vec{d}
\)

Здесь:
— \(-\vec{a}\) — противоположный вектор к \(\vec{a}\), так как он направлен в обратную сторону;
— \(-\vec{b}\) — противоположный вектор к \(\vec{b}\);
— \(\vec{c}\) и \(\vec{d}\) остаются без изменений, так как они направлены в нужную сторону.

Теперь уточним разложение с учетом требования представить вектор \(\vec{XY}\) в виде суммы:

\(
\vec{XY} = -\vec{a} + (-\vec{b}) + \vec{c} + \vec{d}
\)

Таким образом, вектор \(\vec{XY}\) представлен как сумма четырех векторов, где два из них (\(-\vec{a}\) и \(-\vec{b}\)) являются противоположными к исходным.

Ответ:

\(
\vec{XY} = -\vec{a} + (-\vec{b}) + \vec{c} + \vec{d}
\)

Данное разложение соответствует условиям задачи и правилам сложения векторов.