
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 763 Атанасян — Подробные Ответы
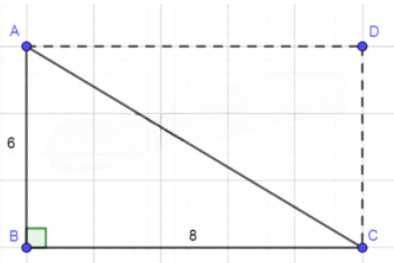
В треугольнике \( ABC \) \( AB = 6 \), \( BC = 8 \), \( \angle B = 90^\circ \). Найдите:
а) \( |\vec{BA}| — |\vec{BC}| \) и \( |\vec{BA} — \vec{BC}| \);
б) \( |\vec{AB}| + |\vec{BC}| \) и \( |\vec{AB} + \vec{BC}| \);
в) \( |\vec{BA}| + |\vec{BC}| \) и \( |\vec{BA} + \vec{BC}| \);
г) \( |\vec{AB}| — |\vec{BC}| \) и \( |\vec{AB} — \vec{BC}| \).
Дано: прямоугольный треугольник \(\triangle ABC\), где \(AB = 6\), \(BC = 8\), \(\angle B = 90^\circ\).
а) Найдем \(|\vec{BA} — \vec{BC}|\).
По теореме Пифагора, \(|AC| = \sqrt{AB^2 + BC^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\).
Ответ: \(10\).
б) Найдем \(|\vec{AB} + \vec{BC}|\).
Также \(|AC| = \sqrt{AB^2 + BC^2} = 10\).
Ответ: \(10\).
в) Найдем \(|\vec{BA} + \vec{BC}|\).
\(|AC| = \sqrt{AB^2 + BC^2} = 10\).
Ответ: \(10\).
г) Найдем \(|\vec{AB} — \vec{BC}|\).
\(|AC| = \sqrt{AB^2 + BC^2} = 10\).
Ответ: \(10\).
д) Найдем \(|\vec{AB} — \vec{AC}|\).
\(|BC| = 8\).
Ответ: \(8\).
Итоговые ответы: а) \(10\), б) \(10\), в) \(10\), г) \(10\), д) \(8\).
Дано: прямоугольный треугольник \( \triangle ABC \), где \( AB = 6 \), \( BC = 8 \), \( \angle B = 90^\circ \).
а) Найдем \( | \vec{BA} — \vec{BC} | \).
Длина векторов:
\(
|BA| = 6, \quad |BC| = 8.
\)
Разность векторов \( \vec{BA} — \vec{BC} \) равна длине гипотенузы \( AC \), так как по правилу треугольника сумма квадратов катетов равна квадрату гипотенузы:
\(
| \vec{BA} — \vec{BC} | = \sqrt{AB^2 + BC^2}.
\)
Подставляем значения:
\(
| \vec{BA} — \vec{BC} | = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10.
\)
Ответ: \( | \vec{BA} — \vec{BC} | = 10 \).
б) Найдем \( | \vec{AB} + \vec{BC} | \).
Длина векторов:
\(
|AB| = 6, \quad |BC| = 8.
\)
Сумма векторов \( \vec{AB} + \vec{BC} \) также равна длине гипотенузы \( AC \), так как треугольник \( \triangle ABC \) прямоугольный:
\(
| \vec{AB} + \vec{BC} | = \sqrt{AB^2 + BC^2}.
\)
Подставляем значения:
\(
| \vec{AB} + \vec{BC} | = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10.
\)
Ответ: \( | \vec{AB} + \vec{BC} | = 10 \).
в) Найдем \( | \vec{BA} + \vec{BC} | \).
Длина векторов:
\(
|BA| = 6, \quad |BC| = 8.
\)
Сумма векторов \( \vec{BA} + \vec{BC} \) равна диагонали параллелограмма, построенного на этих двух векторах. В данном случае это также гипотенуза треугольника \( \triangle ABC \):
\(
| \vec{BA} + \vec{BC} | = \sqrt{AB^2 + BC^2}.
\)
Подставляем значения:
\(
| \vec{BA} + \vec{BC} | = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10.
\)
Ответ: \( | \vec{BA} + \vec{BC} | = 10 \).
г) Найдем \( | \vec{AB} — \vec{BC} | \).
Длина векторов:
\(
|AB| = 6, \quad |BC| = 8.
\)
Разность векторов \( \vec{AB} — \vec{BC} \) равна длине гипотенузы \( AC \), так как по правилу треугольника сумма квадратов катетов равна квадрату гипотенузы:
\(
| \vec{AB} — \vec{BC} | = \sqrt{AB^2 + BC^2}.
\)
Подставляем значения:
\(
| \vec{AB} — \vec{BC} | = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10.
\)
Ответ: \( | \vec{AB} — \vec{BC} | = 10 \).
д) Найдем \( | \vec{AB} — \vec{AC} | \).
Длина векторов:
\(
|AB| = 6, \quad |AC| = 10.
\)
Разность векторов \( \vec{AB} — \vec{AC} \) равна длине стороны \( BC \), так как:
\(
| \vec{AB} — \vec{AC} | = |BC|.
\)
Подставляем значение:
\(
| \vec{AB} — \vec{AC} | = 8.
\)
Ответ: \( | \vec{AB} — \vec{AC} | = 8 \).
Итоговые ответы:
а) \( 10 \),
б) \( 10 \),
в) \( 10 \),
г) \( 10 \),
д) \( 8 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!