ГДЗ по Геометрии 9 класс Номер 762 Атанасян — Подробные Ответы

Сторона равностороннего треугольника \( ABC \) равна \( a \). Найдите:  

а) \( |\vec{AB} + \vec{BC}| \);  

б) \( |\vec{AB} + \vec{AC}| \);  

в) \( |\vec{AB} + \vec{CB}| \);  

г) \( |\vec{BA} — \vec{BC}| \);  

д) \( |\vec{AB} — \vec{AC}| \).

Дано: \( \triangle ABC \) — равносторонний, \( AB = BC = AC = a \).

Найти:
а) \( | \vec{AB} + \vec{BC} | \);
б) \( | \vec{AB} + \vec{AC} | \);
в) \( | \vec{AB} + \vec{CB} | \);
г) \( | \vec{BA} — \vec{BC} | \);
д) \( | \vec{AB} — \vec{AC} | \).

Решение:
а) \( \vec{AB} + \vec{BC} = \vec{AC} \), следовательно:
\(
| \vec{AB} + \vec{BC} | = | \vec{AC} | = a.
\)

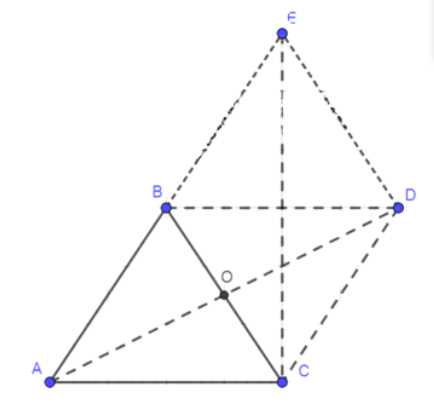
б) \( \vec{AB} + \vec{AC} = \vec{AD} \) (по правилу параллелограмма).
\(
| \vec{AD} | = 2 \cdot AO, \quad AO = \sqrt{a^2 — \left( \frac{a}{2} \right)^2} = \sqrt{\frac{3a^2}{4}} = \frac{a\sqrt{3}}{2},\)
\( \quad | \vec{AD} | = 2 \cdot \frac{a\sqrt{3}}{2} = a\sqrt{3}.
\)

в) \( \vec{AB} + \vec{CB} = \vec{CD} + \vec{DE} = \vec{CE} \).
Так как \( DE \parallel BC \) и \( DE = BC \), то \( CDEB \) — ромб.
Следовательно, \( | \vec{CE} | = | \vec{AD} | = a\sqrt{3} \).

г) \( \vec{BA} — \vec{BC} = \vec{CA} \), следовательно:
\(
| \vec{BA} — \vec{BC} | = | \vec{CA} | = a.
\)

д) \( \vec{AB} — \vec{AC} = \vec{CB} \), следовательно:
\(
| \vec{AB} — \vec{AC} | = | \vec{CB} | = a.
\)

Ответ:
а) \( a \);
б) \( a\sqrt{3} \);
в) \( a\sqrt{3} \);
г) \( a \);
д) \( a \).

Дано: \( \triangle ABC \) — равносторонний треугольник, \( AB = BC = AC = a \).

Требуется найти:
а) \( | \vec{AB} + \vec{BC} | \);
б) \( | \vec{AB} + \vec{AC} | \);
в) \( | \vec{AB} + \vec{CB} | \);
г) \( | \vec{BA} — \vec{BC} | \);
д) \( | \vec{AB} — \vec{AC} | \).

Решение:

а) Рассмотрим сумму \( \vec{AB} + \vec{BC} \).
По правилу треугольника, \( \vec{AB} + \vec{BC} = \vec{AC} \).
Так как треугольник равносторонний, то длина \( |\vec{AC}| = a \).
Следовательно:
\(
| \vec{AB} + \vec{BC} | = |\vec{AC}| = a.
\)

б) Рассмотрим сумму \( \vec{AB} + \vec{AC} \).
Согласно правилу параллелограмма, сумма двух векторов \( \vec{AB} + \vec{AC} \) равна вектору диагонали параллелограмма \( \vec{AD} \).
Найдем длину \( |\vec{AD}| \).
Диагональ \( AD \) равна удвоенной длине высоты \( AO \) треугольника \( \triangle ABC \), так как высота делит сторону \( BC \) пополам.
Найдем \( AO \) по теореме Пифагора:
\(
AO = \sqrt{AB^2 — \left(\frac{BC}{2}\right)^2} = \sqrt{a^2 — \left(\frac{a}{2}\right)^2} = \sqrt{a^2 — \frac{a^2}{4}} = \sqrt{\frac{3a^2}{4}} = \frac{a\sqrt{3}}{2}.
\)
Теперь длина диагонали \( AD \):
\(
|\vec{AD}| = 2 \cdot AO = 2 \cdot \frac{a\sqrt{3}}{2} = a\sqrt{3}.
\)
Следовательно:
\(
| \vec{AB} + \vec{AC} | = |\vec{AD}| = a\sqrt{3}.
\)

в) Рассмотрим сумму \( \vec{AB} + \vec{CB} \).
Обозначим \( \vec{CB} = -\vec{BC} \). Тогда:
\(
\vec{AB} + \vec{CB} = \vec{AB} — \vec{BC}.
\)
Построим параллелограмм \( CDEB \), где \( DE \parallel BC \) и \( DE = BC \).
Так как \( DE \parallel BC \) и \( DE = BC \), то \( CDEB \) — ромб.
Диагональ \( CE \) ромба равна диагонали \( AD \) параллелограмма.
Следовательно, длина \( |\vec{CE}| = |\vec{AD}| = a\sqrt{3} \).
Таким образом:
\(
| \vec{AB} + \vec{CB} | = |\vec{CE}| = a\sqrt{3}.
\)

г) Рассмотрим разность \( \vec{BA} — \vec{BC} \).
Так как \( \vec{BA} = -\vec{AB} \), то:
\(
\vec{BA} — \vec{BC} = -\vec{AB} — \vec{BC}.
\)
По правилу треугольника, сумма \( -\vec{AB} — \vec{BC} \) равна \( \vec{CA} \).
Длина \( |\vec{CA}| = a \), так как треугольник равносторонний.
Следовательно:
\(
| \vec{BA} — \vec{BC} | = |\vec{CA}| = a.
\)

д) Рассмотрим разность \( \vec{AB} — \vec{AC} \).
Так как \( \vec{AB} — \vec{AC} = \vec{CB} \), то:
\(
| \vec{AB} — \vec{AC} | = |\vec{CB}|.
\)
Длина \( |\vec{CB}| = a \), так как треугольник равносторонний.
Следовательно:
\(
| \vec{AB} — \vec{AC} | = |\vec{CB}| = a.
\)

Ответ:
а) \( a \);
б) \( a\sqrt{3} \);
в) \( a\sqrt{3} \);
г) \( a \);
д) \( a \).