ГДЗ по Геометрии 9 класс Номер 761 Атанасян — Подробные Ответы

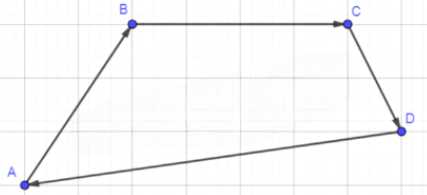
Докажите, что если \( A, B, C \) и \( D \) — произвольные точки, то
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0}.
\]

Дано: \( A, B, C \) и \( D \) — произвольные точки.
Необходимо доказать:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0}.
\]

Решение:
1. По правилу многоугольника:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{AA}.
\]
2. По определению нулевого вектора:
\[
\vec{AA} = \vec{0}.
\]
3. Следовательно:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0}.
\]

Доказано.

Дано: точки \( A, B, C, D \) — произвольные. Необходимо доказать, что сумма векторов, образованных последовательным соединением этих точек, равна нулевому вектору:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0}.
\]

Рассмотрим последовательность действий для доказательства:

1. По определению суммы векторов, если мы последовательно соединяем точки \( A \rightarrow B \rightarrow C \rightarrow D \rightarrow A \), то сумма векторов соответствует перемещению из начальной точки \( A \) обратно в точку \( A \). Это выражается следующим образом:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{AA}.
\]

2. Вектор, соединяющий точку с самой собой, называется нулевым вектором. Следовательно:
\[
\vec{AA} = \vec{0}.
\]

3. Подставляя это значение в выражение, получаем:
\[
\vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0}.
\]

Таким образом, доказательство завершено.

Детализация:
— Вектор \( \vec{AB} \) показывает перемещение из точки \( A \) в точку \( B \).
— Вектор \( \vec{BC} \) показывает перемещение из точки \( B \) в точку \( C \).
— Вектор \( \vec{CD} \) показывает перемещение из точки \( C \) в точку \( D \).
— Вектор \( \vec{DA} \) показывает перемещение из точки \( D \) обратно в точку \( A \).

Сумма этих перемещений возвращает нас в исходную точку \( A \), что и соответствует нулевому вектору.