ГДЗ по Геометрии 9 класс Номер 759 Атанасян — Подробные Ответы

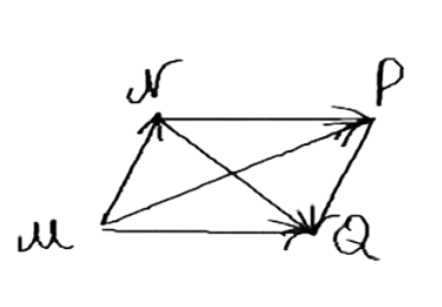
Дан произвольный четырёхугольник \( MNPQ \). Докажите, что:  

а) \( \vec{MN} + \vec{NQ} = \vec{MP} + \vec{PQ} \);  

б) \( \vec{MN} + \vec{NP} = \vec{MQ} + \vec{QP} \).

Дано: \( MNPQ \) — четырёхугольник.
Доказать:
а) \( MN + NQ = MP + PQ \);
б) \( MN + NP = MQ + QP \).

Решение:
а) По правилу треугольника:
\(
MN + NQ = MQ \quad \text{и} \quad MP + PQ = MQ,
\)
следовательно:
\(
MN + NQ = MP + PQ.
\)

б) По правилу треугольника:
\(
MN + NP = MP \quad \text{и} \quad MQ + QP = MP,
\)
следовательно:
\(
MN + NP = MQ + QP.
\)

Дано: \( MNPQ \) — четырёхугольник.
Требуется доказать:
а) \( MN + NQ = MP + PQ \);
б) \( MN + NP = MQ + QP \).

Рассмотрим оба пункта подробно.

а) Докажем, что \( MN + NQ = MP + PQ \).

1. По правилу треугольника для треугольника \( MNQ \):
\(
MN + NQ = MQ.
\)

2. По правилу треугольника для треугольника \( MPQ \):
\(
MP + PQ = MQ.
\)

3. Из равенства \( MN + NQ = MQ \) и \( MP + PQ = MQ \) следует:
\(
MN + NQ = MP + PQ.
\)

Таким образом, первое утверждение доказано.

б) Докажем, что \( MN + NP = MQ + QP \).

1. По правилу треугольника для треугольника \( MNP \):
\(
MN + NP = MP.
\)

2. По правилу треугольника для треугольника \( MQP \):
\(
MQ + QP = MP.
\)

3. Из равенства \( MN + NP = MP \) и \( MQ + QP = MP \) следует:
\(
MN + NP = MQ + QP.
\)

Таким образом, второе утверждение также доказано.

Оба утверждения доказаны, что и требовалось.